ISOMETRI
1. Definisi Isometri
Dalam Geometri Transformasi dikenal beberapa transformasi diantaranya Pergeseran, Rotasi, dan Pencerminan. Pada tiga transformasi ini, ukuran dan bentuk bangun yang telah mengalami transformasi tidak berubah. Hal ini menghasilkan istilah baru bahwa ketiga transformasi itu disebut transformasi yang isometri, suatu istilah yang berasal dari bahasa Yunani yang berarti ”sama luas”.
Definisi:
Misalkan T suatu transformasi , transformasi T ini disebut isometri jika dan hanya jika untuk setiap pasangan titik P dan Q anggota dari bidang Euclides V berlaku dimana
dimana 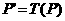 dan
dan  .
.
Untuk memahami definisi di atas perhatikan contoh berikut:
Misalkan garis pada bidang
pada bidang  dan transformasi
dan transformasi  ditetapkan sebagai berikut:
ditetapkan sebagai berikut:
i. Jika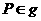 maka
maka 
ii. Jika maka
maka 
Apakah transformasi T ini merupakan suatu isometri?
Penyelesaian:
Ambil dua titik sembarang dan
dan  anggota
anggota ![clip_image010[1] clip_image010[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj3L_sAypN7qy3yp8t1n4gdBRSN5gUTazbYuzhSlVlInsyNszEAWyZfLJU36LFFyBmXugpoc8869mWIsTX4UJWW2L3t6daiCFnjLuxy8e2ahKAfhRUxEx_JKtH2LAk8C2tP_WLkXZ0oyF-8/?imgmax=800) misalkan
misalkan ![clip_image020[1] clip_image020[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjbdh2OnZkNQXjQG1_A6z20lyf6RGYgE_jmtdTSRGKminB7r2noAYF215Nkbj8KzBP17QuJVnsu3ul9LdKDLSQQY0N03z7tuXY6By_NwpwYmRgVliGFEKyY4_AyXFOgQHqVNn2CaAYdHhhG/?imgmax=800) dan
dan  , sehingga diperoleh
, sehingga diperoleh
a. g sumbu dari , misalkan
, misalkan 
 , maka
, maka 
b. g sumbu dari , misalkan
, misalkan 
 , maka
, maka 
Perhatikan gambar berikut ini:

Kemudian pandang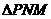 dengan
dengan  . Karena
. Karena  ,
,  (siku-siku), dan
(siku-siku), dan  , maka
, maka ![clip_image046[1] clip_image046[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjjH9sybe-zZsMGDi2LiK9ZyZ3jQaQr4U6WWmDh-MZopOiDWOUxShlIrb_JSccAUBkr6tZ80bV-69xXuTvvCcHFjINYvbo5DMIN5fVTCdG_G5sp_1MdqyBEYRmG90sv-cmrF0MNCfW-jGZ9/?imgmax=800) =
=![clip_image048[1] clip_image048[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjWy0V1VJgNaxUwGVhMlcOpURFQcvdXe3audQUNIHn9TYqC9D72pM4TG6QE2yG6tovzMYo6fnnxfeeLYJoCSGkClH7ylUGG0yH4U1bECQh-TKJUAh2vpH_tHwNvZ5tP37nbk8RrSbC2HIxy/?imgmax=800) . Akibatnya:
. Akibatnya:
a.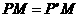
b.
Sekarang pandang dengan
dengan  . Karena
. Karena![clip_image056[1] clip_image056[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjAKmNoLQPIwbl1v9UKCIztC_f05ThPvHZf3UvsWibslxIdzYEqi2ZwU44CGzw5Sym0lpDSIoKnSfud3choBSU4dalvev6yjRk7_FY4q8wS4fsnJaGeGZt4bJWwoH13Q3ybdCxxo_aU_t1A/?imgmax=800) ,
, 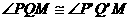 , dan
, dan  , maka
, maka ![clip_image060[1] clip_image060[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgPdlgTcbgXLwWgH8jSje9k6xa8iIN-RYDlAtS4-2moei77whO9BuhLE-3gxPpiQCZ6Ilq3C0L6WviKeiS6-kRJUKGqo8r9Q3aagZFPgW61MXyM7dK8jc5SAj68cH2pITTsc_KD5-JK6XPR/?imgmax=800) =
=![clip_image062[1] clip_image062[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg0iDQzb-Sjk1m_lIHdv2MChbxvg_2V2Q_07pWCcUOb-Vq8kpj1NEO1nCiAVO3Sf5Ff60icTxcZJj-qbeU21ha7ZtvO9yG0rdwQj6ppyZ9cwJxHF1QBdIt0-sfVWrgw8xL9bnfd032PEfXl/?imgmax=800) . Akibatnya
. Akibatnya
Karena![clip_image022[1] clip_image022[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjsrSYGG72RewWahaM_0p8B5QoYzZd51-NoZ81nYuDLBRaax2bH0WwWur12NJ0wF5h8WJM4NVFCuBn5dhMN-vZVfc8WI6KVPezS1ywljYp0cuFdP3KKj_zyBDZqvN7GrKZWQLC7mkH33Xmf/?imgmax=800) dan
dan ![clip_image024[1] clip_image024[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiFeinOf_69YLaUQwfcpQYcHzL8AAdVhYOUFWJaEdpcS3svldui7ayVqjwpjjK_kTnKIisL3kR6cAa_lgN9Bm7dSE48trMukPZNeW06ZX2on0jj7H7dSKTgzvjYglMVYyYCcSb1qj9CaxV3/?imgmax=800) di ambil sembarang titik pada
di ambil sembarang titik pada ![clip_image010[2] clip_image010[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhml9qRX5QSPS_AhqUNQpp1Vec5UM9Na-EfRJT7yqGb0sTKVDOARDwLBDHhUl-1KBx39o0JBoMykvTHioRlH_FYnRUMfKPZj7SVX2aT1m7WU2xBWb6E61RV1WKm0y3LXVTJ-1ebHEWAmUFn/?imgmax=800) dapat di simpulkan bahwa untuk setiap pasangan titik
dapat di simpulkan bahwa untuk setiap pasangan titik ![clip_image022[2] clip_image022[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjkSAa6Lmtm-bpPDLM9mvJceDrqPdOsmHmWRa9NJWdUGIxBj1mciR4pwKXZQNlAiy_vQ87hpmWMzGD6En26H0GP-eoCSUpQ0xqBsyoxpQWfRYVIZ0UgNB2Q-JrULqQ3lhtzsmvbhSTOYsuq/?imgmax=800) dan
dan ![clip_image024[2] clip_image024[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiUrQ5dq88nwlidihHGOJWQDwja3r4rOK767TtF3nt9uaQeIXQmclxQErqXpasTsZAtin_mqI8R0Hv9GkxiDFglukrfGAXILvto-AVJ7M23JWwfMqRzgY0DexkLZyITNbctxPaw8ZD6_AjJ/?imgmax=800) pada
pada ![clip_image010[3] clip_image010[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgSrVoPwqr_gYiZk8v_jmfLe1NTkcKkBIyxL73VLp8RBCXVrhXySL5agC-wBQ8_SOLVvQA_mQB9NsTlQK7P0GA2x3MlzQVCHW5nNyT1Bg7weFZLlrytHoHT-obApJfXSIItsAMH5Iq4-4CU/?imgmax=800) ,diperoleh
,diperoleh ![clip_image070[1] clip_image070[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgssbrQPBOTJ4JK2z03J39GWwzE_FVZB7LdueaxoUi0X5EUn8dNzXc6O0StUJ6fhLUCcQJi_BfBl59dVYEYQrc3Dm4PY1FymtJdGp1vVAKrHU_daksx9iPlYUMCm3DEonhH9qA5miG4DZnt/?imgmax=800) sehingga transformasi
sehingga transformasi ![clip_image012[1] clip_image012[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj_6ZxzEcmOQ-ErAGBn05fOk9dldN4GocQR8UIhq-XpV7Awi2DGPmgACt4wqFvA4JsqJkPRNbH763O84EsXh0L5wejDTDPlk8No_PC-MQg70aH0jJTcstMtLfqknL72OymuLig_RmyOZqje/?imgmax=800) yang ditetapkan di atas adalah suatu isometri.
yang ditetapkan di atas adalah suatu isometri.
Contoh lain:
Asumsi bahwa sebuah sistem koordinat membangun suatu bidang datar dan pemetaan![clip_image012[2] clip_image012[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgWDCIfAh90O9xGl8nRdFmgAuyVt-GiG0pBfbRsPBifnh6JLyTQSiqi57zH7C7d8Y1EhR2hm9YU6Ku7yVuwqQT5NUuiCyw2A394BERJAVreRGN4XRaaEPwcxPxvshh4bsZqqgLI5ifeMs-i/?imgmax=800) didefinisikan untuk suatu titik
didefinisikan untuk suatu titik  oleh:
oleh:  . Maka dapat ditunjukan bahwa
. Maka dapat ditunjukan bahwa ![clip_image012[3] clip_image012[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEge-ssr-k9jOpJ94OSnlfmlLqn8_l3TU1wxI-HCTp5_o1H5PGZK6bPeQr2HoOHKMaC-aS6Z68SBbNl4gPy7zJ-Cmu6j9GyWKp9aeya4UV6LUj6qG0YLlZ6CThXDJW21Ttbpco4m0o_3xou8/?imgmax=800) suatu transformasi menunjukan
suatu transformasi menunjukan ![clip_image012[4] clip_image012[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg5QJyk6l37-5UozBEWp320xa3ZJ9PF_d6Xw_Tgu5cD1HjkNeuySbMfwl2VPsg7oyx-1UPRx68i3FaLZAm44ZZCo4tdu7rtKMoskLGCeOYuoRSiWSahHRrW4zBgDYtiFqCpRo8lRn4NJc0e/?imgmax=800) suatu isometri, ambil sepasang titik
suatu isometri, ambil sepasang titik 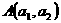 dan
dan 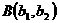 bayangan masing-masing
bayangan masing-masing  dan
dan  kemudian buktinya bahwa
kemudian buktinya bahwa 

Dengan rumus jarak diperoleh:



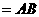
Karena itu,![clip_image012[5] clip_image012[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg3qdVhFhgPHvyLAZpBUUW7sppyh21NPvr4iTYD1mla8n8X6J2QQpHa5kcwO1mpOY0VflayGpmh3ymKmY4jimZ3n0GrbJPLdIRRbDbgi9GciPYDvJP2UPtdjH__6o53wqviGwQw0C-36l0Q/?imgmax=800) adalah isometri.
adalah isometri.
2. Sifat-sifat Isometri
Suatu pencerminan atau refleksi pada sebuah garis![clip_image008[1] clip_image008[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEigPxYYTeFkR-CCuSdKFj-kyQc14G0-ONHGAVi9NCnkTf8QJEne5R10ZUD9Myzlzp8mMYLcJQhtlVqBIcD66q0TEaN1oVmKPHgdHjfk_5YhWHWAT6t2swgICLZmRsRXAaTvMArgsYF4Kcck/?imgmax=800) adalah suatu transformasi yang mengawetkan jarak atau juga dinamakan suatu isometri. Selain mengawetkan jarak antara dua titik, suatu isometri memiliki sifat-sifat seperti yang tertuang dalam teorema berikut.
adalah suatu transformasi yang mengawetkan jarak atau juga dinamakan suatu isometri. Selain mengawetkan jarak antara dua titik, suatu isometri memiliki sifat-sifat seperti yang tertuang dalam teorema berikut.
Teorema 1:
Setiap Isometri bersifat:
a. memetakan garis menjadi garis
b. mengawetkan besarnya sudut antara dua garis
c. mengawetkan kesejajaran dua garis
Bukti:
a. memetakan garis menjadi garis
Andaikan g sebuah garis dan T suatu isometri. Kita akan membuktikan bahwa adalah suatu garis juga.
adalah suatu garis juga.
Ambil dan
dan  . Maka,
. Maka,  ,
, 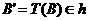 : melalui
: melalui  dan
dan  ada satu garis misalnya
ada satu garis misalnya  . Akan kita buktikan
. Akan kita buktikan  , untuk itu akan dibuktikan
, untuk itu akan dibuktikan  dan
dan 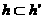 .
.
i. Bukti![clip_image117[1] clip_image117[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg4NVEafn6AiRRNGsihRSdnqfyrKdgrlxlgGdIcyiVzU9ZpxVnQESZY_VkyU4n2b4M4SU-yq3daCtIkG7YhYd9MKRj-5bYLfyxspleORq5mQ1BtnFS9p5jHLVXAyeCnV3gQ4NEwTBPHlzPD/?imgmax=800)
Ambil . Oleh karena bidang kita adalah bidang Euclides. Kita andaikan
. Oleh karena bidang kita adalah bidang Euclides. Kita andaikan  artinya,
artinya,  . Oleh karena
. Oleh karena ![clip_image012[6] clip_image012[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjFLtI-P5b8DpIKQdutRO6JYYqk6wLwa6LVnFL5UB_8jsH1ZqNva9bX8pHSg6m0a8hhkrLCM_RpOQnNkUjkueg_1oaqSAA-8Tygh09uFYe1xAu5VTVT45NqK3ZF6u0ea1Ti9eZcJQuPud1t/?imgmax=800) suatu isometri, jadi T suatu transformasi maka ada
suatu isometri, jadi T suatu transformasi maka ada  sehingga
sehingga  dan oleh karena
dan oleh karena ![clip_image012[7] clip_image012[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjZNE3QLDn09M-_wIZj2yW7cmm73ZLUaL5tqz9A6xYYGppOiMBLFraID28RFcs0CeX27qqDHxhKDHhEjAa-SiSGTn4i77qkZhpDViChnB5O5P2p6f82yNa_TpmKz5LSs08hLaLku_0x69Sl/?imgmax=800) suatu isometri maka
suatu isometri maka  : begitu pula
: begitu pula  . Jadi pula
. Jadi pula 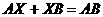 . Ini berarti bahwa
. Ini berarti bahwa 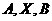 segaris pada
segaris pada ![clip_image008[2] clip_image008[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhzKHq0KYMi1P1wReFmZCzXuvcmanuBzLR0f97saehYRGNQBRixQD428wr8YOoANv80lMF4OXl73ZZ7RG7K-LXn0F5OOIpIRucuhyphenhyphen1WYUnGuOwrSf1FWPEGd3MbDu7bfWnOQm9IGBWLw-Ar/?imgmax=800) dan
dan 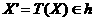 .
.
Sehingga![clip_image117[2] clip_image117[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjaNvxD3sQnglExKpbT7ZHwMczIv0LAuDa085DmLPOKd0Qf1AgBXuSnXOIJrmO4t6LLIuB8jikKl86-Z94YcQCrwvZlKc0sl5ipHBZx-QIJTmKakaQD0xmjjZwr7THV-k34Cq08KapKBGkB/?imgmax=800) sebab bukti serupa berlaku untuk posisi
sebab bukti serupa berlaku untuk posisi  dengan
dengan  atau
atau  .
.
ii. Bukti![clip_image119[1] clip_image119[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj3bEv0S1dOZZmv-uyXEgbYY4ZpFv6Z0dHuHs7SN4agMuSJLA_TJ1qw7qNGduag0D1SaPyPnTdI6zjQw15XWRKDuMmQl0puDFSxMIHTmNvvGNzWPGVmFT1UVVNeivafHQqdaBx-ONqD7ybf/?imgmax=800)
Ambil lagi . Maka ada
. Maka ada  sehingga
sehingga  dengan
dengan  misalnya
misalnya  ., artinya
., artinya ![clip_image152[1] clip_image152[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjsHovAHXwYaKfYi1aJkspBOU-fVRVwVco3-aygVBM_spY4WW2vpqkx-gFjA69urVLveVUi428NjfQ5mdt0vWQi-JKc3Bgmla4IRXUkLoNLWFNsm2NeWMWDOf9K2b_4WyTeZDHtCq9Opbd2/?imgmax=800) dan
dan  . Oleh karena
. Oleh karena ![clip_image012[8] clip_image012[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjWNCmUB4Xs07dNGhl-9QojsCKqJpCQycecdzapoY8YOX4Vv9g5n50_h3C70ONnFShyphenhyphenzjJLARrO3w772B15iuzCudQLzVozJ2ijmOyrp6SELGTfGmGL6NwyNVL3dZuQw-I2GxoF6wIpQEXN/?imgmax=800) sebuah isometri maka
sebuah isometri maka  ,
, 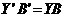 ,
,  . Sehingga
. Sehingga  . Ini berarti bahwa
. Ini berarti bahwa  segaris, yaitu melalui
segaris, yaitu melalui ![clip_image109[1] clip_image109[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjAcSBbePq0c4lfV6zP48rxnvkITgMPiOQsidCD6gbHFVmhddwe20LRTzlJfL1pivwsih9ot6A8s7strP3BS_Rv6S_uv9ccUbKaEXQtQJXwewXb33c-91-UZQa-EMhqc0WBmK7dAtMOwu6R/?imgmax=800) dan
dan ![clip_image111[1] clip_image111[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgXcqZ3jjQmB_OULOQPF1lGHzkSgFJg4KZWcn0Yu_13w_hD26sBlpNC4lylILmuu28LEJjDYNxKCy6GwtNsWVX0XFSud0gD4dbRXyolFvJZ0_ysbyhhh1G-v8rH1cCI4C4P_v7cNDRYsdod/?imgmax=800) . Oleh karena
. Oleh karena ![clip_image113[1] clip_image113[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj-6G9Nf8N__nvBm4d5MXq4zg67aRZkcj9QCbNfftyYZj0hEEGhovG7NAvOaM-HG_QD8kwCHMqN618OsqvQjfhrjUtxaPbyl2UVT2wgquKq-77_KFnYbCQBzGNiv0F8pKqPZlDCwqldwTE9/?imgmax=800) satu-satunya garis yang melalui
satu-satunya garis yang melalui ![clip_image109[2] clip_image109[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj5RCtyGpaMxtrZZAaI1jwJXpmVjMAgAUx9hwji2qel2V0rxKLlG9VUjFGTi77gCsihV63Lorut2HuLUK0KzMcdX2Ns-eYX80nMl0p3xMT9o6cHpvsExVqEeVQbgkeUPDJhlGTxzKjDhi_-/?imgmax=800) dan
dan ![clip_image111[2] clip_image111[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjAEzrtBxSgzMzp4U82dA_jqyJxbjua4Vi8wQhWKVih-IsuTv-VkTmyxhRotnTOyjiRL5ogFthrlufAv9xjhwiNpltJ2ZbQxjqCZWJJuiLyyzqLHgchhdQswAph77pl3dBmJtAi9IsJADKo/?imgmax=800) maka
maka  . Jadi haruslah
. Jadi haruslah ![clip_image119[2] clip_image119[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg7bXRQEnyoU8SusMZgardZhvyQ5xamHHsjBhSRQMWdTzZqPEhYChFeKjFLsxTowCnd-IGFFTetbc6LA5Cj8hSiqJOLyPJfMPNqNEGSvGhPHKyQaLmnm6alM3ur7_BNyT144HA1Nq14Occs/?imgmax=800) .
.
Bukti serupa berlaku untuk keadaan atau
atau 
Sehingga![clip_image115[1] clip_image115[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgfTdRnCrZnO8Wym6JgFzyMOnuhVzh_r9AE1om7tS3xJzWJUCHyT3zqIqZrG-tEtNaGkV4vGOijhyMQ_d6tu_MX6hpv49OvNTTRJ_PZS0YF-rYJT66Le05QvRiTzTgUZ6jeJajOu5u6ZwEO/?imgmax=800) . Jadi jika
. Jadi jika ![clip_image008[3] clip_image008[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhQ4uQQtkmtgZZABbltpPNOVfWw-8c2nbSWK3WZ8pQ1XALUr-JVb0EMQKuhDR3YLa3m3AVwEFEvWW2KU2ZT9iBfRg1tH9TtdONE9rB_mbyDbaNm3du62AYRC6nsBoUYPF7c6i941nywi_eM/?imgmax=800) sebuah garis maka
sebuah garis maka 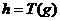 adalah sebuah garis.
adalah sebuah garis.
b. mengawetkan besarnya sudut antara dua garis
Ambil sebuah .
.


Andaikan ,
,  ,
,  . Menurut sifat (a), maka
. Menurut sifat (a), maka  dan
dan  adalah garis lurus. Oleh karena
adalah garis lurus. Oleh karena  maka
maka  sedangkan
sedangkan 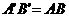 ,
,  ,
,  . Sehingga
. Sehingga 
 . Jadi
. Jadi  .
.
Sehingga suatu isometri mengawetkan besarnya sebuah sudut.
c. mengawetkan kesejajaran dua garis
Kita harus memperlihatkan bahwa //
//  . Andaikan
. Andaikan ![clip_image221[1] clip_image221[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg8H1agbThc6g8OvpIDBw1KtnPEVU-CQIExTOkqboyzwCcSbQL9UKVuAqmaftp5B5FaWSvc4t_LT0lal43AwYVhx4wQDeO6gKqWTNUHMGA839Rd7eqmFFYHx6Ru-rfbxECQazllQcsSMkkj/?imgmax=800) memotong
memotong ![clip_image223[1] clip_image223[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh0eGvreFf4jO9IXqlfT06bItHqyUSYqLN3tOp1E92y2mUZCzoRRsTbgtoAOum7NyEiLBgnxKuCVJRJbX6loRR14UbHP-sR_NQcvCVKutS4u75GCNapZJm0kAmPCAarGo-BYjJT6AnuquWi/?imgmax=800) di sebuah titik
di sebuah titik  , jadi
, jadi 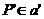 dan
dan  . Oleh karena
. Oleh karena ![clip_image012[9] clip_image012[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhcZ8Yn7tTQ5iaU24UpftHNnM1D8TSlH1RuJ5g7-0L_JoM8n3LSYgzbGdaA7MhGguaO_cigH8kVqEa2efDj6tmNjWw1A2_5qcn_pFdxUelSo_V6Y82B785ZrFStR4w0Bhx5KbuemNwYaYrY/?imgmax=800) sebuah transformasi maka ada
sebuah transformasi maka ada ![clip_image022[3] clip_image022[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEitNkSnW5KIzCFcvUZnDPrLIoX6MnihQTaVqAc9eNgszkij1z7dDqXwvI83OFnR7S5l4lPppvGwKCAg7DdbgqTob4yCxqr-vH-h2GzPxxf9UhRj9YxEoCNYXHnItP6cpKzBmaim85VHzoOp/?imgmax=800) sehingga
sehingga 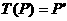 dengan
dengan 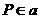 dan
dan  . Ini berarti bahwa
. Ini berarti bahwa  memotong
memotong  di
di ![clip_image022[4] clip_image022[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhoMdqTrp75tSaqxMDbAfTUHK_2WrJ63wneRya1lyWezTXyjbBxVF4RbvpQy536pCuiNaRnBN5s9ggDcYqC-LzyBGTfoiAlrSMzzOVvliwhIVqR5ksegKzusaUAB479qyosGjRz9bIzKa_a/?imgmax=800) , jadi bertentangan dengan yang diketahui bahwa
, jadi bertentangan dengan yang diketahui bahwa ![clip_image239[1] clip_image239[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjOvj7CwgtWCPd_-0Ntwv1kpf2Sh3h_uQv5f5bmcG71HTEWk-cpStMU8Hk4d04j2ymoIPRs7nVQpVrAjitjEbGSofq1C_I6Hjxoemy6XrHNjvNtn3VqJCWIUtJgoqTWpbNY1rB8mjRERdzt/?imgmax=800) //
//![clip_image241[1] clip_image241[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgHDZJnZMNLlTqbKLpVHIc-aDmbD7npOvZsanL7lfMPYk8BQ9Ge3XNLLnCu9871jv_43qrz1IqULBV4t_8cC0TPa3vvmY2Uc6uaNOZZ-IVMqDSaCmVIG5A1drvKCVu3F3RvK8dzycx3ayHE/?imgmax=800) .Maka pengandaian bahwa
.Maka pengandaian bahwa ![clip_image221[2] clip_image221[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj2RqX9IfoNzu01np8oC3yRBFc8mFl9PWaogPlcKYN_vWU3BtqBqKPR42WeqXPegEJXUw9akQhGFSWpOWyxqSSnh4ZbNx1q3Y7bSEzsmMhjfuh__uxSCHpGtV7cL9y7mBWPc3y_fDbZikpr/?imgmax=800) memotong
memotong ![clip_image223[2] clip_image223[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg1OyTMmE5kdEqBBFC05Vx5VsXQGe8Yx5ejxo77QGLmZZ0Bj5FSdG6YD4hramOO7ubzpJZydYDlZ4GlfQpnrbMqW0bZ_ZuBYUJhA6w0AojdE_Sj0egDNgKf3a-tUMskNo3zLJAreGVJnH-I/?imgmax=800) salah. Jadi haruslah
salah. Jadi haruslah ![clip_image221[3] clip_image221[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjwJ6_WAzO2PaSoR-X8UCQpEb7tg6g1k4mKzFnMKMRqP-OiWLLic7pEyfbyL9cMmaK73WgttpUq0MgAJWNDtOq00r6S87wI3aRpnN9OqTqlVphmru2cWgEvdBEM_I9gN7ZTVhIi7rS3Btkg/?imgmax=800) //
// ![clip_image223[3] clip_image223[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhOf6JMeUHbx6WNFG_FTn79u-15gxqigKWgOud1aRy1vhAxbKLayMopzup1tUIALtFmL2d8wzvF9zX-Pdg0v9qlCJi9fo30syeTVl-cQckAMUsHyZ5XwIlD-0Oa_GwKZrn2gD3YQ5j60zp6/?imgmax=800) .
.
Sehingga suatu isometri mengawetkan kesejajaran dua garis.
Akibat:
Salah satu akibat dari sifat (b) teorema 1 ialah bahwa jika dua buah garis misalkan a dan b dimana maka
maka  dengan
dengan ![clip_image012[10] clip_image012[10]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgAJSyL7T6SVsWNooBFaanD4jUQITwnAP1U7yUkmlhwF6haizdFochDqyRgqYSHxoBsbzYIvZdK2Pk5bgbZBTFQA2c7FSL2EoYfmOv2RUV6Qpalyr_FuQ0To19u0YuViqtG10_kiuQNgcVI/?imgmax=800) sebuah isometri.
sebuah isometri.
Bukti:
Dipunyai![clip_image245[1] clip_image245[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhj9VxEdOiwdKJPrftHfTjp6YAXYrPddiGO-UcMbpIW_hhk2RgkrpbCTppJRtVNGFH6GePCwc5ffesZd8_-MnNoUo-UCA2oyDK7cHTGu9x9JBDyXev06oEJCU5eYHTXNnmDHmfFIQLO5SZz/?imgmax=800) akan ditunjukkan
akan ditunjukkan ![clip_image247[1] clip_image247[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiKMStq3Om77iCouCbN0sqmdLkyY2gW-iCoSgnrQHFrMAc0j2FfaHE-9V-4noObxCLFO78DVjt9gyslhd4v2OB-owNE8MhsQqESzTrynxtysDlLP3km-XVUSyY3jfdPrkH1VGTO6J0qXkVG/?imgmax=800) . Andaikan T(a) tidak tegak lurus dengan T(b) maka terapat sudut antara T(a) dengan T(b) yang tidak sama dengan 90o. Karena isometri mengawetkan besarnya sudut antara dua garis maka sudut yang dibentuk oleh a dan b tidak sama dengan 90o. Hal ini kontradiksi dengan
. Andaikan T(a) tidak tegak lurus dengan T(b) maka terapat sudut antara T(a) dengan T(b) yang tidak sama dengan 90o. Karena isometri mengawetkan besarnya sudut antara dua garis maka sudut yang dibentuk oleh a dan b tidak sama dengan 90o. Hal ini kontradiksi dengan ![clip_image245[2] clip_image245[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi-MWu3ZvA06az5lsoxTJ-gR8VG4_nLfbvlMHT3jXthFfEs2wJ1KSZzB8h3R6s70XXV7J47ZP9N_mx6PNaxIP3Cti3VCELxvT8F87FvICLjh-o8HKz99JvegoIKXIPa8DnwmCzSAaPSgl3Q/?imgmax=800) . Jadi pengandaian harus dibatalkan.
. Jadi pengandaian harus dibatalkan.
Artinya![clip_image247[2] clip_image247[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhbzZsM_MqsKOhNM2omkD20fddDXbY9fVL29U7jhp2SzRz4KXDLfP3p2mP5jbrjLTtT0ylpkbP-oKKICN4dQFh9w1DmpHv1KHXJg-BDRX0DEJEjZruv3Jh_PoHSXhF_oNa41QJJBe9zGjcw/?imgmax=800) .
.
Jadi apabila![clip_image245[3] clip_image245[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjxPUeR8kZoWswu7DkwT2YrIc5SY9EeIC3mdFU4tk-CNPCN5646iZvN6MIpf95m_9_PngQlBlwoyX1F6ffjiuumhtWAyI8KeFh-extIVssZwu5HinVQb7STTy8-esW9Z4xUV8Pm_D7imoHS/?imgmax=800) maka
maka ![clip_image247[3] clip_image247[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiUwN7QxJdS_klkAsR07Q8axRY9wwrr34iwtk56_lgXnBTp_7Qjb58YtYE8I3ADlf7FTZ3_qpqrL6twGPWD4fSx_FGFnM1lB04KBVRkq-Rdc7W8pyqF20UAanNgOi58f9easPj2ocriWYaK/?imgmax=800) dengan T sebuah isometri.
dengan T sebuah isometri.
Teorema 2:
Komposisi dua buah isometri adalah isometri
Bukti:
Ambil dua isometri, namakan dengan dan
dan  , terjadilah komposisi dari
, terjadilah komposisi dari ![clip_image249[1] clip_image249[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj7MEzhhI3hOXsG2-miCLpMVIsAesTB2jxvTnEhO0MO7ATEhqi6O04g51xgonxnpeGBnPCL6G6wr3u_jxZ5EaK4q1rvNaPKMPzHtNnyyEk02KjjnYfzKoPso-FP2a8zJEOKKor6lKK87sKa/?imgmax=800) dan
dan ![clip_image251[1] clip_image251[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgHxsm65b9TleAI8udSdf9THmIb8JiU0JgdfgDFJtEJ102HgyOBImvOhoCC_WKQE9yZMfSrRlm0ANfAPr0FIZMgREYuP0Vxd4ACnShNBjxLM6bIlmkAsEOTP5aax57oCQK_s489P_MfEdt7/?imgmax=800) .
.
Yaitu dan
dan  . Dalam uraian ini akan ditunjukkan salah satu saja
. Dalam uraian ini akan ditunjukkan salah satu saja ![clip_image255[1] clip_image255[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEibNeEY0wBHKYVOwubR_ON153SsY5wN2Ob3vYyxlm8sQxckQqlDhqRw0lzYi45qZFtoHz9Kw6so5wSBHVBEGBq7SqY5eGaTFPLhWSCeO48ciQVEhtXFUbFIH7GcinaZddf_8kvpDG6svKVq/?imgmax=800) . Ambil dua titik sembarang
. Ambil dua titik sembarang  , misalkan
, misalkan 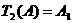 ,
,  dan
dan  ,
,  , berdasarkan pemisalan ini dapat dicari:
, berdasarkan pemisalan ini dapat dicari:


Karena![clip_image251[2] clip_image251[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjaG2U_WwVOz04cp7Hv4Gb5toWLx47SyUUmvIG56-PR1RRQGF65QKU6v4QFUGK3OITXPtX5ncMEL4LHzoOZG9ZJ0whdxNN6vQcHP9-uLfgmTvVOScksPaHBdwjVjbtNdHwYgo_HypaSXs2v/?imgmax=800) isometri maka
isometri maka  dan karena
dan karena ![clip_image249[2] clip_image249[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgJpUEalc1r8vDrGkoEG2EO8sBY2E2teOjIH3zRDMiYUXagNssJyXXbjvpU-qAur2VqMsf_eA1oizLN8ptsJz92VTCImw9EpN37JqQIZ-5O5T-hL4Hb3bihl4NpFq2D6EdVQileYbWx7xUr/?imgmax=800) isometri pula
isometri pula  . Karena
. Karena ![clip_image275[1] clip_image275[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgzJYMDunWQ-SLizCda5TeoT4DJzuHtaeVU7KyuGCEhO9aiIY6gdXiHxKKPv1JTE0Zib4K5er7Em26ra4TVme3CYYTBL3aX1d-Fmj_tLNI9cLarbRYFkkoFOB3G9wMkIo4wdF_cywxLq0Ok/?imgmax=800) dan
dan ![clip_image273[1] clip_image273[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhA5YT3HumVCpxEF5tjz_RMa7552Wy6ph1UZxPpeBZ9XGwrI4enYmzNGhoOFzGezhfhMoZ_gwksi7SbAY0ZvvEURaMUebAKGV1iq5wl-Rg0xn0R4sYH37nquwdEukHneq1f9G0jn1tZdTQX/?imgmax=800) , maka
, maka ![clip_image087[1] clip_image087[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjrun4pqSeOvsXOSVRdm3QsSwBJNueNu8n0sBM09JdGhNYgPjphZ73bEaVl07Cw-BxOhuUS88z6AHM0NqgOye-ik2vhuZb_Uf7yUvgGngSSxC1uKNb6dQqQa5DcZ0_eHHzgUS8fAPKJ0ggm/?imgmax=800) . Jadi
. Jadi ![clip_image255[2] clip_image255[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgPI73LrK1SjTGbt08my_NpTayJX_DpkYao6L6mrNk1xL8qdmz9uYork6vIy4wonU-7-BH2OvbiebmQmoWHnNyiCgqlPpanU725xQQnL2iPhT5tREfyFMclNzH9H_SYu1q8ooG5Jitjf4T4/?imgmax=800) suatu isometri.
suatu isometri.
Soal Latihan
1. Diketahui garis-garis s, t, u dan titik A,B seperti dapat dilihat pada gambar di bawah ini.![clip_image012[11] clip_image012[11]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjqAnh679y8Lfqyv0AIZjjUJN0DklCDNDYWStTG2pZU72wXeDMvBbTCH79AFNY7JCwYZzT6xQowlB_vpmpQcHkoTpO-k-I0fLJe1vzImL8SH5DTl7v9Ch9t7zJMvyluxYUcadz24_VbtWv2/?imgmax=800) adalah sebuah isometri dengan
adalah sebuah isometri dengan  dan
dan  . Jika
. Jika 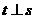 lukislah
lukislah  !
!

2. Diketahui garis dan
dan  . Tulislah sebuah persamaan garis
. Tulislah sebuah persamaan garis 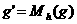 !
!
3. Diketahui lima garis g, g’, h, h’, dan k sehingga dan
dan  . Apabila
. Apabila  buktikan
buktikan  !
!
4. Diketahui garis-garis g,h, dan h’ sehingga apakah ungkapan di bawah ini benar?
apakah ungkapan di bawah ini benar?
a. Jika maka
maka 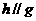 .
.
b. Jika maka
maka  .
.
c. Jika , maka
, maka ![clip_image101[1] clip_image101[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhHkdWjbyOvVnGafqt3cWog15Df1lor5bUW7kmiEOiMr_ne6qmlcBSds2UG8H0p_J1f9doouv5Mezj0b-BW4xHdaz4Hqt5o2AW0SoqHfE9w0GSuVTxq0mE1OqkkVOQlMQPBunABXrME_16O/?imgmax=800) .
.
5. Jika![clip_image214[1] clip_image214[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEivm7nRUPgNOqhk37kMwetn3tUz7CLnf18XvKa9DvQqp65OOVW7THTVpVc6iHB2CVM6vKjqq1OTsL8gymiOBnjT0cEd29dqLnrQA1whyrY3070hCMCgJ1MBWmeCiOMQ7aY6fLU1VrsezrYB/?imgmax=800)
 dan
dan  , selidikilah apakah
, selidikilah apakah  terletak pada garis
terletak pada garis  .
.
Pembahasan
1. ,
, 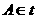 . Karena
. Karena  maka
maka 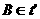
![clip_image286[1] clip_image286[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi3B0UFMUrscIUc8p-Bg3pEwl_e1lytWYNrk_uxenpOF8HDtEPfLIL9Bn7QCAiTESWACXqZ5iHJq-L5g27DBRsXkPxA3K-32E7uTVgRK3ceKMpeHPObEuLXYjW9TDad5Y72H5IkD9cuZH5X/?imgmax=800) dan T isometri, maka
dan T isometri, maka  atau
atau  .
.
Gambar:

2. Diketahui garis![clip_image290[1] clip_image290[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgQxsDh2wI6kLG2SBVFdrPCkOYTjDJzKROST21nWOukGQXbf8toOAkGYvzJISfz75j9ejr6ZIlvSh9boJZa4svIa3TedTT_Y2yoErAp_Ss1DJrZw6ziCFoiS5CNInVKJmK_Es2TBwpwx7QV/?imgmax=800) dan
dan ![clip_image292[1] clip_image292[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjJPPQc82p3o0Uuww7C4-_RYwDEf6TqrJ_HaIRoiVM8aLfHgGdgHlmz1DgehNRw40mo3KYLTRc96kOkUh1Z0E9TzB5N-sCb9G3NlchISHM21w911Q9t_vwRxAJBORt98dsGIvY6vpdA0CWi/?imgmax=800)
Gambar:

Karena sebuah refleksi pada
sebuah refleksi pada  , maka merupakan isometri.
, maka merupakan isometri.
Jadi, menurut teorema ”sebuah isometri memetakan garis menjadi garis”, dan , maka
, maka  adalah sebuah garis.
adalah sebuah garis.
Titik merupakan titik potong antara garis
merupakan titik potong antara garis ![clip_image008[4] clip_image008[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhrdOFaSqOG0tnfUXve9-sPW8BjEajZf1xFW-znCN1uSOVIXAmOnmhQwhZSFhEFPMrQf5pI2kbL6CPyyJLALMQc04WgQNanvrMb7FveAh8K3dgMWWIsWWR9Lu-8V1v1Ak6ZzzF5hD0GQKM7/?imgmax=800) dan sumbu
dan sumbu  .
.
Titik merupakan titik potong antara garis
merupakan titik potong antara garis ![clip_image008[5] clip_image008[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjW2eiZ0YQyHzZii-mklSdtzHVAXFJ-OodWgLlZTXu5QCZix0IRn_Deomvju-FJnFQrk25LpThyphenhyphenc8fMVYowXW0_9GWev-dOmaoGCfFWXWKf7W350qtvyA5oS4E5pFG5KEkuSyBswVGcgPKi/?imgmax=800) dan
dan ![clip_image341[1] clip_image341[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg9mUE5aj19BPjHsVks0WyGne2b9mUGHoUSVKIRYDFkeHFuPhrNnJ6qVk2GTuB0bwpT3mVJzaOces1dBYuGN8i2b17ovvb3fEBL6z1HbnRdlY8KkfFBS0V9A2eSRkQeK6urEZaQD2E7IqEL/?imgmax=800) .
.
Jadi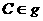 dan
dan  .
.
Karena![clip_image357[1] clip_image357[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjrRlgTw_ewDXoZdPfy8DlpRw7bXFjIFT-iGfoLDAlHltdQHhaIBmzJfDA71FsG4MTU2RzAcLe7gtvmQHJaSWHRkpa2FsIbGlUuF6G7i8QLeOuZjTHDl_50i9QzZ7dxATz9I5sFSNDcpQg-/?imgmax=800) maka
maka 
Jadi![clip_image345[1] clip_image345[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiDDEl3htautNsYfcO0AX3YqDToatplEp09JzP7Pigtnbf3Z0G32AE5O9QtCkxPbn_P7LRzodz6zNlseFrDPmqs9-JjCGO7XNWmKlunXcw7YQKoQlzcH2kQdk2_nMhCMhvyZwaTZrpZ-3HM/?imgmax=800) akan melalui titik
akan melalui titik ![clip_image352[1] clip_image352[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEift-nVPZcTnx-NZ50v3LRO2HEPrey4V5PBqSc2j-Pq3Sj9ru-k3AyyK1jxEyXD0MscL3reXTScomPznThe7MkBrG8n78My_PbkbP_frS8sk9F6PoJxIXQGGJ6ctEGpOCqXawaIXlWG5b76/?imgmax=800) , dan
, dan ![clip_image345[2] clip_image345[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEieCTk1M3qx5kF8quqg1OonntIiFSF6w8SeB3Xil1o_J5wHhhQiZbVOaGNZKNn55vkUKnnVzgETa3_Fta5lhnTLLf5jTlzqcvNjmHY5O2DIo4mK13woYFRJpWfj2mzJ3e9RZbFRrID4f3p9/?imgmax=800) akan melalui
akan melalui 
§ Koordinat titik![clip_image352[2] clip_image352[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEguC8irrM8LBBSvoCbTekekMm8ZgXs74XCthsmiTxiHBPhOhJyIGcCKHPEOGvb8ELFmwa0fSvizIBxySj-ZiKlxakZ4x4GOBE5_MbVSOg2UPIsBg_OBJiuajvX97G7yl4ltRRpTOGeZ65vK/?imgmax=800)
g : x + 2y = 1 x + 2y – 1 = 0,
x + 2y – 1 = 0,
h : x = -1
substitusikan x = -1 ke persamaan garis g : x + 2y = 1, diperoleh:
-1 + 2y – 1 = 0
2y = 2
y = 1
Jadi
§ Koordinat titik![clip_image365[1] clip_image365[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiuRt0OBQXJ-tz7d0eR7Pm8WvFcR4vVTsUyVkMTKq05z3_UFy-uozs3lmIs_q1EG5A-BNTzMpCQ0u3Q-0wMkKBr5svnfTmTiPLSQArvhZu6b1Zfia2HWWPbvbDv5-UgMJaVHvZBZWpJoCuV/?imgmax=800)
Titik adalah titik potong
adalah titik potong ![clip_image341[2] clip_image341[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhg_CTgWSbFuqz77AEBir8XCYi2BH2ve8GOQFp1Wh7aUgzlm9RE2aGdEprqtqXWXRoQzPLUG3mLTpD1FFYX6-uY82dT1H2gEJXUyyr4T8FSGe_0aCHJj4-YW2BdRZhQJWfLBw6wGGMUjfG7/?imgmax=800) dengan sumbu
dengan sumbu ![clip_image350[1] clip_image350[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgONq2SvVfA2cE9kUEZRUMVfh_leiuddcrHQdpeHgXbiV7dfJl8OfMp_znllTTZLxUaxqiGUNr1RqTAZTOg-YD93iD-uchBwI9n0yrz7jgzpZJ7l9QMdU3F0Ss3Xmb4WjLs6PO3-CWJBneG/?imgmax=800) .
.

Karena isometri maka
Jadi,
Misal titik
Absis titik![clip_image109[3] clip_image109[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi4XeSj9xiZPTgWIdus1abm-kH4vlUWYV2b7F2Db9THEwnVS4CjWUGTssEY-vuPKAkNYMrwds4zpc8EyBbHE_UBF-ntvSokjNSH1UvUzVhxwc3tDxkSMdK-qNb6eZo2M4zfEzF8ttCenpqd/?imgmax=800) adalah
adalah 
Diperoleh dan
dan 
Jadi,
Jadi, g’ melalui titik C(-1,1) dan![clip_image390[1] clip_image390[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiA9lsqdjmiuekGR2d-M_ji2nsgjJviNqoikCv8x1OHFa9YTjEC6Jd9ZPXl84tIqbqTx2axtfyH0_PkQU2yF2qa19Q5HTdETP5SvB1gfd6WxJHbWYMpYaWNzzUIiCfb2uSHZw1BB-6fEG0r/?imgmax=800)
Persamaan garis g’: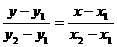




Jadi,
3. Diketahui![clip_image300[1] clip_image300[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjbBpfFbing_mNfaNrvyA7rqMV95xsghlicOOnWQzVHjK_tbea9q7Cdhk9RQZEw2ElRT6I0h_9UYUl7OHNwky0f1atvLZME50jrL6RzxFb6GmouGH2CjXi7PwGKWD3H8LE46jmCrpnS1iuO/?imgmax=800)
Andaikan g tidak sejajar h, maka menurut teorema, bahwa isometri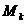 mengawetkan kesejajaran 2 garis, diperoleh
mengawetkan kesejajaran 2 garis, diperoleh ![clip_image345[3] clip_image345[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhHDGnmO5W9ssC9oFAJuYkoT5f-yink-poPQmrpdxxzQDV844Q3sU11Q3zV2FerVDNVbWn5vzxbDcfaj3AE4i-rJmUkEQO1YJtdacIrYkKlnYOxKPCWeeYS_OnHYPToFAPg0sMGUhsunI0H/?imgmax=800) tidak sejajar dengan
tidak sejajar dengan ![clip_image113[2] clip_image113[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgfgSCcIy7fI8_EXf-1Izhm8VLk21t7Uka3EaFi2QYOzHg0Qli_dMwP13WUXCmBpVuib_fFY0-JkIY8GcrTXYT7Qt97iuLi_Zf4Py06A5ydeXC_4t3cK3fHsY01G90eqze8JbtRhyphenhyphenDKubzL/?imgmax=800) . Padahal diketahui bahwa
. Padahal diketahui bahwa ![clip_image300[2] clip_image300[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgimzxGtyUaoaWdUlu1n3uO-NSydZeNgyvxv-BgMPq17UOavNBDkcQI-3_7zJRkOUNK2L5RRV3coaVtJ536fD892wZlqk9IWGPb-cq5q7jj95ukJ8koYVibH4SZcGO0uyXDN4txS74b-ln5/?imgmax=800) , maka pengandaian harus dibatalkan, artinya
, maka pengandaian harus dibatalkan, artinya  .
.
4. Diketahui garis-garis![clip_image008[6] clip_image008[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg1J7C8fUg3Hv71erPyXPwxYrYCi1qUneid26o110wDNGKzgzOxEWMlZ9iJEirYBsm-28XpCy7Tl8IL6pKARhM-n08e2uv5crK6fzyU5kEkgcyKqQt-WQeRymOsHNtcDpad-NsptmSh4lQA/?imgmax=800) ,
, ![clip_image341[3] clip_image341[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg8e1FmJdeBkqB2_ffhHqAxP1L7DQmOIeHKp5Sc-TD3RgthJgZoEXsb9D7YOykXQTHwG-3Q-v4j_S-tFg96dVRNFpnNNq-9kb1yYmUsRjEePLAtcB8-E0FDg2o4MZWF2AcySvQbJKMY0275/?imgmax=800) , dan
, dan ![clip_image113[3] clip_image113[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi91jUcjN2PQq7eDLgBaQi8jrdmJsL9MXX1sSwpU_iU7okGjh2IoevnvDanBuKCyHslzfo_GNnfRr7r5GXH_V6070c9QDRnMbi7cNrb7VWLlbrksKEryTO4i9OAOkxN7oicjwRji-VcKF_m/?imgmax=800) sehingga
sehingga ![clip_image304[1] clip_image304[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjdYNdAbDXene5nkrISrhbKvmkz9DRRifOeV5RgX6D70IgUdJQ0gZs_5M2Cel4KQdNae4TvjF68sI9vqj1krYLjH2LjVXSUWYRp7QJayBKD1Hkhb84nX-haRUJhKPYd7-ZgzBzjkbzjafUZ/?imgmax=800)
a. Jika![clip_image306[1] clip_image306[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjRbLlxwuHg0fkajQ8ghgsjsgwYURzs0TKq4sdOQ7bc3QexvrSYRB0oqPICdRjg_8JC1TeqrJce89ak_A-X7dQ97CtaKdYhaHpbiYp2OvBQLaigFXQR3ANBG-sQESiCoN4KOlsduRgOCS7h/?imgmax=800) maka
maka ![clip_image308[1] clip_image308[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEij-pw8i0Q1Y52F7s0X45FKHMwf4Vz3dXqjL9INWDJne0ffX7wXvd9y8IeX4AidBTW1PKSobikAdWXVrJgIC25ilPrL8kpwPViE5s-nJ6HWWuyjXXAh2SQuF3smziPr77ERisgcILbIV7Bv/?imgmax=800) .
.

Jadi benar jika![clip_image306[2] clip_image306[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjPzTsBradXUpmoT2dDWv9yu9zCKDbmq-CwLE-KfAlS87_88ThuefQbuoLbDJISXHrXbRaI01Y7314p4uUeP0KOFzMWXYvpPbwyRNTzMuqCMESqVaq7S8Kw4sWfSbEQ3SLuUCVQDU5TmIK3/?imgmax=800) maka
maka ![clip_image308[2] clip_image308[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhvOwpx7aLchywm7JvywgFNdwpC01k21NEluBSTbVH-RkYAsuYKp1TBgZqAtol8Aw4RocZfMXbr1JcBMzdbc695njhYiHCZj8bKQsytmUVsl6fKzc04MqyQjywcFE5t-ZQE8IUSwoycvdvC/?imgmax=800) .
.
b. Jika![clip_image310[1] clip_image310[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj0hgI9PrfMSS8wgxZXK6jY-u9_YdnWe7LAaMIKr-fw0uvm5WGK1b92jPlLI-qDBfqVLKKQfzxZVX5TlSY4LESTIhOhXx0ZxWQviB0PHwpbAk2fQw5p-v8mDRwslg4F_1rMGtbywLlE_XFe/?imgmax=800) maka
maka ![clip_image312[1] clip_image312[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi9a7dHRTvypPHtDgRyovaHCoKU6ACT26x03RdOA3cBcANfVPSIMDy_D_bqZcsC3u3fo7TQQXRtI_THyAdxl9Im2qfp8KJHO7AFKtFffAV3kNHuNEHg52dfDflu0YBZ08j4JxHR5Za2tVNW/?imgmax=800) .
.
Jadi benar jika![clip_image310[2] clip_image310[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj0_bpJu7bGDFXo_wnyzF63M8gw2SZKbobVYPTw8TdptoHbfMfnJKms7tlXiZEYBOVLBNqKPBUVWU6DlmG9F5EOOrDpInMPlQfx9jHJn6HxIQ-gPNx8UV5HzDYY3MCZAoYy-1D30pcq2qkx/?imgmax=800) maka
maka ![clip_image312[2] clip_image312[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgKPQw7YZI2mwRgkrUcJU7ItFZVwqciKgKt1Yd6LWp5km-GZfIOWuKAyoUep3DYemmI8oQ36tbcsYSrU8dSdtx9S-ZIZooIiG0cuv05tX0XpjvdWfAks-8fMrTm9MiNwxhX7R4tDawnYavf/?imgmax=800) .
.
c. Jika![clip_image314[1] clip_image314[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjdAvNfpBVqKG2CEjB75c9QE2rT38nuflwPWYWMiYbqFo2juumfIcDH8O9CJjA9pGcOyT2onjVPsXZFlOuLKJCsscbR_9VXSgjORg_WlQsHgjnicLRbUm4mrg1JjzWIGTIB7gELezZghZ_I/?imgmax=800) , maka
, maka ![clip_image101[2] clip_image101[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiSlmnyD3Ar1bYx27UwM7qCXwSgZUCnpQA-aJrX1a-qtSTB3eFOzPO1J-EVIYw0935pnYp57L-kbFiSefd3fwP6QTLW7M1Ra-SRobT6R8Ps_2chWhaz4NjF-4D9ah42TiyAcSnojlovDvpA/?imgmax=800) .
.
Jadi benar jika![clip_image314[2] clip_image314[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhWa6zjlM3kJUsBd1Drp2z5-os50HKsmwO0026xmHGhO_5cfgHvBc1NCldJU3k4X9PZkZXRV2WlO4ssT_hlGgS3AXj3f0hCvU4GlCsoo1Sgec-4m5qOpVAq9AUTGJDwoz3yFmn3b4z6YO1s/?imgmax=800) , maka
, maka ![clip_image101[3] clip_image101[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhHU9j1RPBiATss66US4mxKQDwu2WROglMpxr4ACMhB7sAppCcqtCU3uJ-754NuacvY2hseHIlMtlHo3jj89b7eW15MD4m1-M3IerfibdxNKcN2zwBS4maJKG8-LD4FfLaibny0iz_gpYTR/?imgmax=800) .
.
5. Jika g = {(x,y) | y = -x} dan h = {(x,y) |3y = x + 3}
Gambar:

Karena sebuah refleksi pada
sebuah refleksi pada ![clip_image341[4] clip_image341[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgU7jliiOg3ndPmjJS-8c66DNyR6Th28JBzirYuc9fK6yVHoPWCm6V7-ZT83guESsWL3usN4YM3QQkZwqnK8Jef98QI96A2TXWp5tO4vGrhDLjAQKVCzpQj1zqCponE00Iq2qXLALndk1mS/?imgmax=800) maka merupakan isometri.
maka merupakan isometri.
Menurut teorema, “ Sebuah isometri memetakan garis menjadi garis ”, dan , maka
, maka ![clip_image113[4] clip_image113[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgZ6wikdPR45KYSV8_lpjjNx9-A7hphyphenhyphen30vQvBEQAREhlWD51VIQkzscMCzb-Rg0HZ4w0R_EBXWnoYUCfEuELRryiTKqJhoChxlQ4l9ldRCvmJ8CftYhRGgMbSQGPlTS3CtowEQpmvm5_Pp/?imgmax=800) adalah sebuah garis.
adalah sebuah garis.
Titik![clip_image352[3] clip_image352[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhkluZeKxD-x6bjtyy0N7vw8n1tGc48CKgp1rDzno5JnUvgAMMCOJo1u9ylp9L5Vt1ZOLEGz-kY0tPuxYIByMirljkFCfDE9AUegkm5reyfAGKU0qsb6k8yI2gpFOLdA_tzUeguMtHJxSL9/?imgmax=800) merupakan titik potong antara garis g dan h.
merupakan titik potong antara garis g dan h.
Jadi,![clip_image355[1] clip_image355[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhy3k6dhwrgvmAxf0YRBKm9TdckXnbSagkgxTtTRoFblCgAnDe_ywC6YZsp90LCYltRSIBK0IsRJPOkhbCAgcXVmI49abyz_c9ueNGs_xX6luVia05I0N0hC7FQbvaJtkTacdnuFORXEdaM/?imgmax=800) dan
dan ![clip_image357[2] clip_image357[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh07_ZYD5LA7-PkFKjnFwGrQFyw8POkIass3oW18kFIcC-fGU6ZydiCIDJUfOJoy2xS9s_n6gXwhrsWLCknCYCqerwwfujU291VLtEvsDnOEFXu_bvUYe1qWzPltjwC0OyljikkkGwHCYgb/?imgmax=800) .
.
Karena![clip_image355[2] clip_image355[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiJPiqWKsYUOa9C8S5uTLZMQsgzvIHiDSsafIfdxW6L1NT1DpbmrEjxzI_Pz9sH1GGhfV13r7C4i-bDfHPKuFSaiVYM_2vl6fu76mzfbR8CNKpxav-ysSYCmR_XULJdvLIFaePUoBRF-Kkg/?imgmax=800) maka
maka 
Jadi h’ akan melalui titik![clip_image352[4] clip_image352[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhRYJCGuS1gDI8RDcoz44M1KgUcC6u4DzK21kX0Ndlzm4MWzK9gJzyweDtfsZH7Ku1VZ1ZhSyavh8Wh6W_WLPHnJKDr62qHioTcAVREDlqLbYryQ5B7Msdt17MLa9f2R2q7311LLGS8n3rQ/?imgmax=800)
Ambil titik A(0,1) dan B(-3,0) karena maka
maka  dan
dan  .
.
Jadi![clip_image113[5] clip_image113[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiqFOwiMDFlYnlurM3iqcVeg3yynGmXYnCWDmfvY6bivGb9s0oWTJbz-vs5lrJSSVmQggA1p7iB_Ye2z4Kedpfj09kPktMNoV58NcESgf1hUKwQtfiSgu_jADEBh9x0rlbihvU1kDgwZTjl/?imgmax=800) melalui
melalui ![clip_image109[4] clip_image109[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiQF7c-3nJg7VLBAVN7JUZmym7dcXEF-n2i6qBReXAgtAFnObAOx5fH2fjdLMBwGn4_98qV57nZiq2ZLKCsN__fxhnIVOvvRs683LAsroQ7sJ_qe4hNS4i7YYy95fLLitC1j_AETS6j-lUi/?imgmax=800) dan
dan ![clip_image111[3] clip_image111[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhKFOkUlaWJOEdHJI4vplBz6h6INyj7Wcb_XiuQ4-_o26wtENYqM2F3dqdqRJsfn3CF24Q4_TSjCkOAcVKk3MHIG-HWZ-hYLzrXiWLJAIhpwi7hlCebKzSSS8C5pYRV5s0bjfI68yzcspOj/?imgmax=800) . Dimana pencerminan pada garis
. Dimana pencerminan pada garis  berlaku misalkan
berlaku misalkan 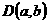 maka bayangannya
maka bayangannya  . Sehingga
. Sehingga  dan
dan  .
.
Persamaan garis h’:![clip_image393[1] clip_image393[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhalCJXnEin_vTr4TUiEg6NHWHTUVbDuMPLraNj6eR3t6CUuzxDEQWx7nUhyphenhyphenyVHI3Z755LwAVIZpEVg1PoQpckb8yb0UO6LsIdo9q3WrRb49zN6IMq036Mxx6U4tGBrPyH9pSTcqTuo5tMT/?imgmax=800)



Jadi persamaan garis
II.2. Isometri Langsung Dan Isometri Lawan
Untuk lebih memahami isometri langsung dan isometri lawan terlebih dahulu kita bahas fenomena isometri yang diperlihatkan pada gambar berikut .

Pada gambar 1 tampak bahwa apabila pada segitiga ABC yang dicerminkan pada garis g dimana, urutan kelilingnya A→B→C adalah berlawanan dengan putaran jarum jam menghasilkan peta yaitu segitiga
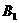
 yang urutan kelilingnya
yang urutan kelilingnya ![clip_image458[1] clip_image458[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh6ne8L_a9qVF5dXtFmVeqSgKVm7GyL7NJZvk-vbHxO59TbbzeBzrZUWBR02htwLY7FXwFoar-sNFdrOt_deZIjggn26UO09lIgjNOOTPCM0FyH3T8qSsFknSrgGmPWyep27DFSW5PmfWAs/?imgmax=800) →
→![clip_image460[1] clip_image460[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhAulpUUMzkl8Id2W1ykrbiU0EkKkr1PtbQ3LMgXF3zysoTgaaANpgNzkZOIa_4phUFsu_M2psKwy365ltUemh1YSkUeYuZbDh9G2lzuS0LsRy4kVwnn-9CmeI7-XmH2BkfjRLuw_RQQxcG/?imgmax=800) →
→![clip_image462[1] clip_image462[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEijUSrZ0kmNqxzI3nkADSq9DFcs5LBml6_rqp370RWMgN2XmS0ygQcXss5Mi85Tfmb5GxLlNEahub_P6bYRgyAeuWe3uqmyd7m-YLJrdcqCAHVURwUP6vNbRbhpcvrmfKOtRZwCMaQuMVjA/?imgmax=800) adalah sesuai dengan jarum jam.
adalah sesuai dengan jarum jam.
Pada gambar 2 dapat dilihat lihat sebagai isometri yaitu suatu rotasi (putaran) segitiga ABC yang mengelilingi titik O. Dimana, pada segitiga ABC urutan keliling adalah A→B→C adalah berlawanan dengan putaran jarum jam dirotasikan mengelilingi titik O yang menghasilkan peta yaitu segitiga
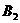
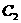 dengan urutan keliling
dengan urutan keliling ![clip_image467[1] clip_image467[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjX_2A9r8K1OgpkQ2ckJdmma7jaqbhx0UMMIWdtYUmm8C_t7XeQxg7Fen3Ol3u8v4Jj_bsEC9hQAX-jdDQOG5vsvDv28d5b5vbA3QCdrqfAxEqcWtDVsMONAOJoj4eIwNcNJMTw4jqRyy4m/?imgmax=800) →
→![clip_image469[1] clip_image469[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjoC6N8SzgiEBg14sPv8VRvtLjQ-h8jmvENKNN9yzblKsyDTGVNa5x0dj69biZRD12DpQSyZZf_KXIp3rZLKzltuo0FjdSQQ4kPJIA6ZOBWWs0BGGUS4PeU7XkTGqDzZTfW_T1JnYY6kekp/?imgmax=800) →
→![clip_image471[1] clip_image471[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhKzSADYo11B4Pi_qU-wj6HgcJnFmxnODxkGOrhXdwdIUtdvB_R0KYjX2yTfirejMceWRn8eHJ5eoHRSb1KeXCIpbxX6f8qarn6jEQzBwoH4tqIjbQef658U4gbSa2n3Ueebc_ABtjeAr7-/?imgmax=800) adalah tetap berlawanan dengan putaran jarum jam.
adalah tetap berlawanan dengan putaran jarum jam.
Untuk membahas lebih lanjut fenomena isometri di atas, kita gunakan konsep tiga titik yang tak segaris. Andaikan (P1,P2,P3) tiga titik yang tak segaris maka melalui P1,P2 dan P3 ada tepat satu lingkaran l, kita dapat mengelilingi l berawal misalnya dari P1 kemudian sampai di P2 , P3 dan akhirnya kembali ke P1. Apabila arah keliling ini sesuai dengan putaran jarum jam maka dikatakan bahwa tiga titik (P1,P2,P3) memiliki orientasi yang sesuai dengan putaran jarum jam (orientasi yang negatif), apabila arah keliling itu berlawanan dengan putaran jarum jam maka dikatakan bahwa tiga titik (P1,P2,P3) memiliki orientasi yang berlawanan denga putaran jarum jam (orientasi yang positif), jadi pada gambar 1, (A,B,C) memiliki orientasi positif sedangkan (A1,B1,C1)memiliki orientasi yang negatif, pada gambar 2 orientasi (A,B,C) adalah positif dan orientasi (A2,B2,C2) tetap positif, jadi pencerminan pada gambar 1 mengubah orientasi sedangkan putaran pada gambar 2 mengawetkan orientasi.
Definisi:
1. Suatu transformasi T mengawetkan suatu orientasi apabila untuk setiap tiga titik tak segaris ( ,
, ,
, ) orientasinya sama dengan (
) orientasinya sama dengan ( ,
, ,
, ) dengan
) dengan ![clip_image482[1] clip_image482[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi4xldiKG_ZULuPy9vRRtN6fPBdwAS4k2QTbli6PCbjbfCsQ68hHMPCJUspyyVUNSeDNIXVJwArL_ceNbDb2aABszNnkbTUiefy5fiCSjJv_VvaXdK5Ju1dXkxOd1NeGWLbErT40J1tBRdp/?imgmax=800) = T (
= T (![clip_image476[1] clip_image476[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiEBFvBpkpUB1lcKc7jcqum5ss6x_13CqarD_jVNNbxZ6ZVgvh6-GgqlRmpOIEiv34bTx4i7CeaWJ9JI6HDVLKCi_mP6Ru6X4YMQ_630zPLXD50fznuBgXbCxWo7iXvpmUxVACZg8aZFYNn/?imgmax=800) ) ,
) , ![clip_image484[1] clip_image484[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhh-bCd9edVT3373b_HJzuD-UhAQKvBcJPsHGLViirIrHGQ3BdcpF08DhMPu1tGRMELNyniclJ-TJRea_CwL0MDidN5sUA5neV96xCQCAWwjtwbwMKAaO3Hi4ic1AMUil-oC6Lmx8TeXKW1/?imgmax=800) = T (
= T (![clip_image478[1] clip_image478[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhO7mNaiNi0gKqhZ3qJs-jpRUyVfsPV4hmxIH0SouxxyCEfn1IxqZYSDYEVS9Z_ErFvGox7Y1RToz-4VsunGDLewbpfmNl2DVbdXRsA2SSwZN1DdrA2dZDbzi7OYmR1xV2FfnkNjgVv-9nN/?imgmax=800) ) ,
) , ![clip_image486[1] clip_image486[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgyIgLO5gsVby8cOHcmiN7Qg13HzqZ39APffA_ehf_H4g2xodzg3PEDKoK2l3GVKGlo8Lrt0U5blK7JfVEw3p-lukeoq81rr7DX-eC0aLx-5nu4Xt1n5yRtUJcx1BonsLihoFkdeHA59tuj/?imgmax=800) = T(
= T(![clip_image480[1] clip_image480[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgRT-Uirm2GqINwauOfxiCv72gm-fQQsiCkd_3-8l1mOjcnHSe5m1t1fnm_xd4z5RtdXoEQrvz675Esl9FM3qkyrlBN1154VpsTJfNT8M20IJUnONCqkSzSVZ7ot1zId1tyZGX-tdG9EEFE/?imgmax=800) ).
).
2. Suatu transformasi T membalik suatu orientasi apabila untuk setiap tiga titik yang tak segaris (![clip_image476[2] clip_image476[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg1NmWAYglYlA4tnoA0V9_c6lGh0jyYAnuwGniwAvjdEwrIER4w0KI3tczNnzdgXNgOKVWiiFrF8Vz2Ka65d6jdx_urJZvnenej4pSttnw6G3_jNjUn-iUZ93OV41jytW94jS3qbC8kGzvC/?imgmax=800) ,
,![clip_image478[2] clip_image478[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiBon90aHJ0DZUp-f7vjxoHjzdcZMIl3p80-3b-7m0-Rjm5p6yq49dMZaK0-VbOM26QG8vHWvUdAqqgKmAI-I4X6zft7azkoFgd6LRchzaLfiWE6wqY5QHtzRy5yXuTn4wVodiSgWJBZnjT/?imgmax=800) ,
,![clip_image480[2] clip_image480[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgZCe8_r0AXUo78meOyUSP67dATCrJIJCUDmMfzLam5XCQegWdHvXvqB2l8iXpxC3KJKpgwgnwoYoBQ9UsljoXfIVc83uHTVJrPveBIAytccwUJ7DIM8qqva4J2-dN2gqp_7kMjMvpr76jb/?imgmax=800) ) orientasinya tidak sama dengan orientasi peta-petanya (
) orientasinya tidak sama dengan orientasi peta-petanya (![clip_image482[2] clip_image482[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiDk1X0mR6B7uUler98AFOblSI1dHsec-GljhSrx23fwVmHT2yqInilb8i2HFi46jtyfgDxo9sPpFM4j0_rS6bY0Ve6iCLFf1-eehaitsCadut0SeLotU0WpbE7ZMFDgvo2bWAxiGV5nJ8s/?imgmax=800) ,
,![clip_image484[2] clip_image484[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgYnJEmmQq1f8UQY74gG0g5jLSCkLANvwiuFYlcIdM9HdTXnIX46FfB7ty-hnvZ23nIiPytUGvrxniEXwZCh6yEjKuHVzDNMhf9iixn82yvWK0yX2YE7Qoj_1KbM78hnr9A-nEtEjZZ2DAX/?imgmax=800) ,
,![clip_image486[2] clip_image486[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiDLRnEANy4Jwhc5cXjk6mvtFg4UUl-j-RN7zHnzWVIls7T8NE-7Nx-EaUgtlIWd2Iu2sPilglnw3X2bmvkYNcXE5pG05cFs_7An_GAErtCSB3HAAuPEnAQ_PeyTkmxxjHtHbxMvmJiULsJ/?imgmax=800) ) dengan
) dengan  ,
,  ,
,  .
.
Definisi:
Suatu transformasi dinamakan langsung apabila trasformasi tersebut mengawetkan orientasi, suatu transformasi disebut transformasi lawan apabila transformasi tersebut mengubah orientasi.
Salah satu sifat penting dalam geometri transformasi adalah:
Teorema 3:
Setiap refleksi pada garis adalah isometri lawan.
Teorema 4 tanpa bukti, tidak setiap isometri adalah isometri lawan. Hal ini dapat dilihat pada gambar 2, dimana isometri (yaitu rotasi pada titik O) adalah sebuah isometri langsung. Oleh karena itu dapat kita kemukakan teorema berikut, tanpa bukti yaitu :
Teorema 4 :
Setiap isometri adalah sebuah isometri langsung atau sebuah isometri lawan.
Soal Latihan :
1. Pada gambar berikut, terdapat tiga titik tak segaris yaitu![clip_image022[5] clip_image022[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgTKQhjO5SAF10v_pyto2v-hYpc4uZ6-ntHx7rg-THBDR4V-5rlqBW8pyVPFkEPlN6ZQr3yGmJt_JjiORIlWvT5o2c-TA1OpT0mRzEyCy-D7tNt2iJufpoac7Vy6TguM1LgEMFU9g7nXkGk/?imgmax=800) ,
, ![clip_image024[3] clip_image024[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg5udMILDQrekq6JKYNqGIGaetI7G1GSo_8Ee3roNIC0Co0cs2SKOlp-4Kfkn7sX3DwTGd4HJZvF6h3GpSpkE8OtJ-dM1HMVY3_xmNPG7VjWEs9o5-VOlIXhOzsP5ExJwYrYVamDfRrYNBg/?imgmax=800) ,
,  ,
, ![clip_image012[12] clip_image012[12]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEinJoQgnNNM5qlgbezyjHsODhjPxv7GxuWYSQ79eDSI9ZsL8BycT0i4R5lgbZhCTdY7stMI4q4ZAbmfWdMCUi-C8IrOtCGFr4lKEKFHEpEemY_erZ2tX6NKp_6DLtF-ofsKgwlZDdGY7340/?imgmax=800) dan
dan  adalah isometri-isometri dengan
adalah isometri-isometri dengan  ,
,  ,
,  sedangkan
sedangkan 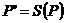 ,
,  ,
,  . Termasuk golongan manakah
. Termasuk golongan manakah ![clip_image012[13] clip_image012[13]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg8-Dk_f5vSvu9kAUCDZYP4r8QioH2nkeBA-nTyV7r5IaeiwHiiDUKgK1VRePeo6ihEFvIpGa1Vyb-tS4zaAUuTxbZC-qNeb5GbnxAygyXdy6nFlT2uUerK8C8EBtbUDtqcI2fjKYtpx4Gf/?imgmax=800) dan
dan ![clip_image513[1] clip_image513[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEipTezwocmZ2fjPGZGv18zh7dWxizyPsJrORayJQZLwWsbpWq2K5PkUDP1puEVDI3R3iaSrNZ1rKRD-qz75iOZmaqokL_-Usl2TyryFZ6S3m0yj7Q8DZvh8OzGhimJXlC882_RgeU7d_lb7/?imgmax=800) itu ?
itu ?
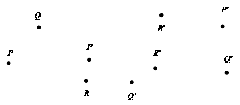
2. Isometri![clip_image012[14] clip_image012[14]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgQN8pQ2K15TQIwBvoYdpMgWYOo3Fhfhn_Bwi22eCMFHwxiwRpU_VvO_7P7pLHEfYUdIyZwBCbId-06Bie76RArGp1sKjo4TvuKgsT2aSil-myq4ed5dCGivWFEB9Ji9Mxrf1adOJlZcNN1/?imgmax=800) memetakan
memetakan  pada
pada ![clip_image128[1] clip_image128[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiP57vDOJ-_QlXK10prZTe1K8g4gf176lSRPnFnEXzMO2wTPadh3IVj2TS8LpFXDYvoLhf9bh-_6TeMEdPNm7VfnKNf6A89F3w82NV1ou8HiRoR79vPYiN4_Sq66D53ONWPGNtMLtTDGueY/?imgmax=800) ,
,  pada
pada ![clip_image156[1] clip_image156[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEju-RU37VnV-VVTe5PYHau5tWAXLRr_Wg14NAeYcq1aliFaDySS_1fsTII3eS_nrc5UnwT2jVz9xU5MKHSUQ8qV8p-TbNNiDl9yEXS5j6cfxhi1XEOuTlSSgyxPHn1QmSMVUTb3g705_B9r/?imgmax=800) dan
dan ![clip_image352[5] clip_image352[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgxFHGwMIccayzuotlovvrpC2-XA1vP_GWX-_i8l_KEalsSZbpA3_kelE5NrStEU7AcdrLRETp3ZnKYSvzqL4tj0O7g1Tv0tdSOfnHhgRRX4Y5Q_JCneGToiFFeBst9-83YLDdv_qERrGYL/?imgmax=800) pada
pada 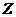 , apabila
, apabila ![clip_image012[15] clip_image012[15]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjgTu_ajyPeVqsX2DNifkEYaLWvu2EK0xuWq-QKts9RDfPvnin7aVrkDj35GDFWLVoW2l9qrg78DVN3ieHw3b6zsxsI0c-t-leWJMS3WuGrbB9s0YpkaD_Msjr81T6CuH6tDSELBptdHCOH/?imgmax=800) sebuah isometri lawan tentukan titik
sebuah isometri lawan tentukan titik ![clip_image541[1] clip_image541[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi87ofS_0fmBcHZjbNLx7yAoDEbqYpaQ9ZOcoVmGO5WetLCrL2PO-MjWW6WSzGTsrThuWheQz039KnI8D4aYdII7hlPKd39IKpegtmlLuRWI9wIUNDWFMsIip3rtD19bIphRFqVFKpWl33d/?imgmax=800) !
!

3. Sebuah isometri![clip_image513[2] clip_image513[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi7SCidH_wzA3PjvK1qldAQJSQ02NeoBa50Pn_w568R5er0HgP2sIMWKAUEGtCPtojL6nLnkOeotArzTrqUqTlJXQlx2ZigVQjkxBv5-SESXqBLCaXZt1xO1DjaWzKCzoEebtOuUA9c0FIZ/?imgmax=800) memetakan
memetakan 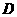 pada
pada  ,
,  pada
pada ![clip_image541[2] clip_image541[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcscW8BuRCJ9lMk56UxrxES_HQ3arZLMlGt53VpR-PziXrAmekYaUVw3P7QGc3pecGQCrkc4a3IOFSfI_GfHkdw4n1ayafnAN8ZuGzfOxiQPp-U9Xkvmh1E7q0GSkMCxSMKM2_98GkqKnw/?imgmax=800) dan
dan 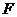 pada
pada  , apabila
, apabila ![clip_image513[3] clip_image513[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi8dflsC8UigiWscaa3Ae81W-6NbYYWshvV6hfUajX0NdlkM0qH93OVvrj15Y1rHqSyERD7pYCXMQ_065Dcbq_Zu4CYvJsshNzNVyatig17OzMnfh3wK9NIwDNFpKr4Bh5M_qDyWx6fxmkM/?imgmax=800) sebuah isometri langsung tentukan
sebuah isometri langsung tentukan ![clip_image552[1] clip_image552[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjuif0PRMd73HLZ5qU0HTVmEk84bYyry_9-gYLgt_annNMsmovEKtNlIRmNnjPltc7kxX2-JQdr5sBM7z1ztZqD6yJrNgdAdxTwuQwT8dGv9giXIgMWW7UHrYEnsX_NBi61avi1sYPb9TrP/?imgmax=800) .
.
4. Diketahui garis-garis![clip_image008[7] clip_image008[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhRDBKWktDgnjg6pB6eL0Wadswb0nbu6xQTgVTmbUawd-YgyTbCjFMAEEGhoYgCwWwjYoUaH0y8CfB91m3TYonUPZfTYKK5WspHTdfLNYkF8Svum65SfkdFxSbbbXEO8GUjTzvRZr1A3Hza/?imgmax=800) dan
dan ![clip_image341[5] clip_image341[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgxZvb_9jloGbSNQPOrs9ksWA_cwAeAWh7FICqk20l-RUDvZEScdaVqFyqpoblVfqSq8QVoSl0mu_7GzyiuhGUEpWWM0_x9A4VzHlJJB2C61rkUenaoMB0MoITn4Gl2mzCyMH7KT9tljVe6/?imgmax=800) dan titik-titik
dan titik-titik ![clip_image022[6] clip_image022[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg7Ua6YR0sml9NfFmZLuPHVbxOmZYc7Fk-1IIZye-AYWYhrkX4CxdY07I4xHWK2NkAI4eoAavz42b9F6Prmk0te8R2CvUVP9oiwG2sVELM9fKl4OTVxv9GHGhtCbL98GQsZJMJjo0Hcmdam/?imgmax=800) dan
dan ![clip_image024[4] clip_image024[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj2H9BNSLA0ewhpryAyHRjaN4LZ_pl-0GUBOH777QCous9diQp8-nWWWxH-COpV3eCPPsvY2-c_AoYswOkW9Eef402F8UvttbvLdlwl-Z1_6obmtIssCQY0Ee4WXeM4HeTNdgjbhbINkn2o/?imgmax=800) .
.

Diketahui pula bahwa ,
, ![clip_image571[1] clip_image571[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjllojbn7TZmGxbjwDhSvJGEtU_RCLl6MMisJKl8qv3K_T5sowAGd4yPhPRjy3uxa4XVicOu4zTNs6DBS6YulHtk2Oj0ei_KSPV960Zui6MWo7zpxiCKpCTrS-bwIpF3IcZQGaqUpBERNuL/?imgmax=800) ,
,  , dan
, dan  .
.
a. Lukislah dan
dan 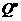 !
!
b. Bandingkan jarak dan
dan  .
.
Pembahasan:
1.
Gambar:
Dari gambar di atas dapat diketahui bahwa ![clip_image012[16] clip_image012[16]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgeJtpptiiVlBHr5Gjvr-zuHWPv26MwvGP-eARybv0J0_mplIn8T4to2B9dr4DqywFu8vLq6MpbxoFU8zigWfnAYRxfies3JzrR4uXUP-LgwkVe2di8jLocRpGS0aphWzRDIs4YFj2FMsn_/?imgmax=800) merupakan isometri lawan karena
merupakan isometri lawan karena ![clip_image012[17] clip_image012[17]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgajMvXtKSQucaWiwarHWKUsD7PPsiBJr_qJbER2aqEpkbfflexJssLW-aPHBfBvYu2c-Dg72EB2_0fOgVT7lB0egScjEcOuKR3yRBX6oxdyH-TjWbE6tnC5UXeD8yKaqb2lZAnRkxI2sqN/?imgmax=800) mengubah orientasi
mengubah orientasi ![clip_image022[7] clip_image022[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgBq48yzBrWyQ7t6at6FgtKH231Ts8YXzQ_CXcQjpNMfCDqsTIQSM975wu6xrWv8Hi2kINbs8VxeWuYOdoF6G44O74zuYg97ArOijzVUUFss6uNLMkAKrJXky-C-HEhntvg4R8FyfjN12_L/?imgmax=800) ,
, ![clip_image024[5] clip_image024[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg5FygTm0Bi2MP2-VI-40IaoK6rldT19tqYZ0fVX-MldWuSe8AVyK1A91U6r7zGXI7bCnfXGRXPVS1J_u3DsUHxxjI3QbSTGw_DPcTS4OsKe_4BdjTTN_mHs2yyu2HJpsV4hDs1WE8hEs-U/?imgmax=800) , dan
, dan ![clip_image510[2] clip_image510[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi4a48p0Nk-Gr27b3r3nQ_vduk1c7YSd1FCxdSP9mPD695ig2oVhHa6Cp4N1pzhJifLvpYH_mu6sF0ZWU-3PLDMFLYacqQCY4hIO9FQx70rgIUNtfqaM59QcFEbav1b7wKBWwYNCy7pcOqh/?imgmax=800) .
. ![clip_image513[4] clip_image513[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi-SpmouAthf4dD54GAq4ZpcOT_QuqcLjZYqtaaC3TbW2ngDxLgIYCBC-xG-zGTRHzdRMhe2z28TTCpYskzag99ynNCPOCSl4PyyxMQb2AA1VRT1YuCpW2HO9lkop_9_QpX7MVIoaIe3Ojl/?imgmax=800) merupakan isometri langsung karena
merupakan isometri langsung karena ![clip_image012[18] clip_image012[18]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjY0LPkajjts_G0mpJe4VuNuFeTCyWR3w_4FWemE22GX6ldUMcePAm-4mF8qOz-jM_xW8_jmyvZR69Urx6wvsqrXUDZ6KCwioByTDowEMN-eem8rF9pXCC6ZJH4Hp2CKxgO9UnY4gR7RGRK/?imgmax=800) mengawetkan orientasi
mengawetkan orientasi ![clip_image022[8] clip_image022[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgsS9tjU3hukebpbaAdzBen6ZwqnsRWDHp8RHUdmFUM1xHfNXjnKndefMItOqDv4nYhAkeWdmCs7Cc8b7L52vm2WJ6BAyFaWBWOSAuP5VhzpMUP99WNrp0LXsZSoVoBy3SV4M0j8cBBwHv7/?imgmax=800) ,
, ![clip_image024[6] clip_image024[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj3avCkYT3wC6AIkCxQctEIt6L0MS4fMrtBMq2cpj6uucNYHQaA5DMgHQ2eMW-fr8wPnC7vKZAVUhkvQXXupJWBPeaR8vW_kLFE3GPmtUJ7f3zI70M30mFPe0CvJeF8wBtnlmOo5eBmrgKq/?imgmax=800) , dan
, dan ![clip_image510[3] clip_image510[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiXcWtEqsjUp5C0kl7tvHvay-bf_VE9_ci6l_oX7Jkf0krLioIxuTGMUdnqPrEjlIBe9YB2w4xmxJ7yBWOb99AGThKjP__s4VEueJRCF171Uvkh1ApcfTm7_JPLke_IwAS61Gg9KzS4lL65/?imgmax=800) .
.
2. Karena![clip_image012[19] clip_image012[19]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhrSiDgXcGsXlSPNUAWiqgAS1EtnDD6gyH973VNV1qDp_mrV8IenLT9FedJOG_TtDE9_s5ed-igmlHvgZM1zUXvO6JMMUEE00f04PCwbqMrBwynbmoFkwzBbhs1UILyRaxJE_hATqBSQIQG/?imgmax=800) sebuah isometri lawan maka
sebuah isometri lawan maka ![clip_image012[20] clip_image012[20]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg1vKxWtrTXX_846ihMPR1eKRamytUej2HXdU6E1S7A_DX7BH6x29fFNy5_xDH6AV7-mi6O3qmTtmPcH5qYqCR_IatubChw6JwrMirs50Wmc46mMgp7mzZ1jFmKkEYcD7uQqrTtMnNDNTOu/?imgmax=800) mengubah orientasi
mengubah orientasi ![clip_image534[1] clip_image534[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjtSOc3M9MJmERyDXo6BlCi6f4wbTtnen7xaKRfgQJsEA5RgNvQDRKcB8Nl0K6rgYi3Wmlv96jrmslwTb_b05JzVXMu_Bz9KsAOpQmSPzi0grZ6Q4hzV5W8WcA0wE0K1gopWLG1kE6JdZsy/?imgmax=800) ,
, ![clip_image537[1] clip_image537[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjYILxlhyphenhyphenc0fOKxvfzUWX8ywt8chlUImAnG23ObkR9HD2mpuxr5gDIhEfLiam1ECzlDjekT4tvjP8L3pwdUYqlm3paj6Q5cgeS6BEgU5t0IkKIA0Cjbhe70_GET_DefiXGBTzxWlBJCmHKs/?imgmax=800) , dan
, dan ![clip_image352[6] clip_image352[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjj0t7PImF2Gz6GA05SV7bB4TIDgknsFBUtw0U1t3PB7Uq0IOfpZXz60VoSjE3uNaA6UFL8a5F6lwjKmZok6vBVgAlMAP8s_EBHHmQ4LJeDHsEqrFCez8FE7C2UDISHmLGKfVHkor_auHZh/?imgmax=800) sehingga
sehingga ![clip_image541[3] clip_image541[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi9Dh1UtXaGS257fWr_G7QOwpHBPJ1wq4NBvvhfsfvLoYRXezAm1wonbSlWYUx3jnHTbFpGLJPhB4SaKoykzpPiwJFw51MSF6Of6sGb7BGd7zA39FraPvMI2BoiZZLskZIrJIMMU3423jCy/?imgmax=800) dipetakan sesuai dengan gambar berikut:
dipetakan sesuai dengan gambar berikut:
3. Karena![clip_image513[5] clip_image513[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhwkABHhXD3AxFVRk1ToRPT7AC9cqNt1ALiD4ayc_AbR2yot2VLvW5wS572gDMtrTpUecM3M31Ql7qFBHR-eMzwofLdqrpU3LZ3GQgC5nIRVEffwnvJrwLipzz3IEDU3dCSIY76A9niDn7g/?imgmax=800) sebuah isometri lawan maka
sebuah isometri lawan maka ![clip_image012[21] clip_image012[21]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg-WIpQyZCbX71hkDwsIZ0NFt0Ev7nwBkkUEd_kW_hu3uAp23tYywhBp7cBksxwVTGOH9Uomjo-tqEJ8EjNWFc8vc6tNcRAhyM6JS5sfGAljv7ISSzGFO-Xm2vQ1a8zVPvcludmC9tRBGpv/?imgmax=800) mengubah orientasi
mengubah orientasi ![clip_image543[1] clip_image543[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj85zue1Q743AhGsgMUtufPDld3nqmbEEhBPrXHeFd4KPI56HolbtosJ4DzBe7kCurSgUcICI-F7nrshT9nyLWP3MN43d8uJ7tjzxy3mBAKH_ukWjmhwe8pRXlYF5EqjGC0nJN7m69o785v/?imgmax=800) ,
, ![clip_image547[1] clip_image547[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjgWQocvyqdkEr-XaRFUFSeCefMxkolycj4c_D04UdggP39M0WtnfuP1_DobsZ3xTMI1BfaPg3BWHvuMcYRtOvX9F5SgFXvEg1W29eBhimqPB7-_XH_mLGyANXJghMuBuDpiQ5KiFb6Ec6o/?imgmax=800) , dan
, dan ![clip_image550[1] clip_image550[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgy0w0_gErGk3RoagJwXhxHpKrYTjAJgIS9lAQa4TDHGi_gaNJaU119xFRgMmN0I-ExDX-JM3yh8rrqC-vz3JgF03TShyhgVVR7QhceS-y_CO0k7ischFk5NOUHmuNrYQgXfWpuXMzMunpB/?imgmax=800) sehingga
sehingga ![clip_image552[2] clip_image552[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgSwGOgFHZwIkfAC1m1g6AbM8_j7E8fGIP6FoF9gUf5u4oWOrRZ3Qd94kf9AK4YOnezXv1UpOpbDo0tJe1bhuaUSOXjulrK35BAa1HWSBVwa7UPAw4TIt2ui3PccqJ8Q-TU9xkCuP4mutJi/?imgmax=800) dipetakan sesuai dengan gambar berikut:
dipetakan sesuai dengan gambar berikut:
4. a. Gambar:

b. Karena (isometri mengawetkan jarak)
(isometri mengawetkan jarak)
Maka jarak![clip_image225[1] clip_image225[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgvK8CZS8xI7MBUZdGcP9OH6lV_viXobcak-WfAF0RBeymTHcLiwIePf03MeBGQZhw8Fhlig88IcNYtItYae0QmSIUq-wHbCOIJ0n93vjinPzNWueoycFYhQ1nZpEN9EmEEIGcI7tXCXXEU/?imgmax=800) dengan
dengan ![clip_image341[6] clip_image341[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEih1ZCKYvqwjqK5wl6XGMGtTi3W0mUuXxWwR06GXyBQ2Uskfd9gY-wANpwr_w-Nvu_jA7OLS03P2awlVgbQz8zQiKR-p8AACCC5U_UwG39SaULye3XQmT2RdiPtkYXUoMjygGx9CZ2aVlVh/?imgmax=800) = jarak
= jarak ![clip_image578[1] clip_image578[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiOuIEW7d_IVi9A8nmqslstyQZ5LCeEheLcRxdk5urfCJJOllH0-k7-ZhUknooKSiJdfn44TKf0RUCltoZNHINkitwgk8V6WcPd-bpTKuXfn9wFAlHv-0AzC9pASySB4k3KDboiuZvsJTNm/?imgmax=800) dengan
dengan ![clip_image341[7] clip_image341[7]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhk2QXpR8ddrJdUsO5xnOtJTCiKWsAuQqL1VXynwp_rUX-xrJ-LoJyG9DwrL7K8aE3H8Y0Rz3QrFgKFuiPqtnGOZOGOTPXlFAmUNrREy3AadYaddKCAHk8Ff1jsLQCCY6ofQjYpsARpP5Tr/?imgmax=800)
Jarak![clip_image585[1] clip_image585[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjIjD-JwDEnsN-bKeejef05tRTJqWBtr5zYoiV_rxS2rePl3qmZASZ6jB_EyDJ9ASHeqwBs9dBg0o5eD7tNly6cyM0bnzCxerE2egpW5Ni-wxDvsqByLz9TXIxIO0JWxFKBb8LmrISUmv4N/?imgmax=800) dengan
dengan ![clip_image341[8] clip_image341[8]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg2WEteRTUfpmCj2FJAfo2yaSJhLuxIMwRFRLrbRBiEpncVpnwsvIiXgXYFQW-EnDzFFSWvrVr-3rwY8tTlyGqohCcsfgiN_iRQIO0iSXvP93mgUIdJfpoOT7IYKYv6BVsFaNW3785m2ZWS/?imgmax=800) = jarak
= jarak  dengan
dengan ![clip_image341[9] clip_image341[9]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiUNmIYBD7344kqxBCcF10VSc42YP34mVAeHpl-O-bDhFDsfC6b0dKRWoMXY5jn3nL5ehQR4QiRcjC8BIdiSu9gT_fbR3kagmFE-tf584grcYvp52t0unXqHggZBeDl0kdkZ3aD1Ume4-x5/?imgmax=800)
Jadi jarak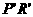 = jarak
= jarak 
Karena jarak = jarak
= jarak ![clip_image624[1] clip_image624[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjhlkFcUz6ZWN7a2sfjTFfTx0rK0qiWExw7E7GglT_5u3vKsFF6qrtgHHUdrHsjrTjEVHIE81BttqkQ2WlWx62QiAXq_Me1F-qm78JrvYbQGd6jiTRuAv319roDNEgQEHDt7Qa28yE58SNx/?imgmax=800) dan jarak
dan jarak ![clip_image624[2] clip_image624[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjURpLGIgNgcj9XFk0qLXJaJVHQh41YQg13iu9uRbXb0L9jGeWxBd_b3AHouxPyBN0lfmPzc61tQgifgbhJkeTtInfKGdSTRaSK2npbn3Mre8xmoYQ_XCm20LSnqU7cKW9U2mTIc7oIc863/?imgmax=800) = jarak
= jarak ![clip_image626[1] clip_image626[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiyaBdoZv3THFLZ5jZ-ott-bUFrqt3k76gfuCSqRbpTlkUFv5crR0L0_7HwVRkpHCVdVKUv-9bFXLtj_rCIujGNIFC3P80vvqWE7PCCSsAwtmndpJu_CXdZlpjaV5nDv6tc7N0HXNVvwHsn/?imgmax=800) , maka jarak
, maka jarak ![clip_image628[1] clip_image628[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEieh4Kz1ZbQpxVBKRxdVVgLEFZxXNvPFtD_2kfdup1bTaGHvFo-wAY5z44UdQQ7T4fhc2HVkpC4Qxf2ZozyxMcebYzmiKmVPr8NIK7yVrX4c9pWcfOoydPwsNfAiPVN-DzFc9oYyNB3nv8T/?imgmax=800) = jarak
= jarak ![clip_image626[2] clip_image626[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEguENZInL5jzDZjYLR81WUFHAH1NNrft1NlScd0covVA3lPH_uo6S2-MtaSovNEdH6kJM_EuoqQ6xUvXSCOfbBWn920XHeBw-Yluqg6C31BhyphenhyphenO5RwQ0ALfIWP9_bSjVbaRSz0RLDflIqK6U/?imgmax=800) .
.
Dalam Geometri Transformasi dikenal beberapa transformasi diantaranya Pergeseran, Rotasi, dan Pencerminan. Pada tiga transformasi ini, ukuran dan bentuk bangun yang telah mengalami transformasi tidak berubah. Hal ini menghasilkan istilah baru bahwa ketiga transformasi itu disebut transformasi yang isometri, suatu istilah yang berasal dari bahasa Yunani yang berarti ”sama luas”.
Definisi:
Misalkan T suatu transformasi , transformasi T ini disebut isometri jika dan hanya jika untuk setiap pasangan titik P dan Q anggota dari bidang Euclides V berlaku
Untuk memahami definisi di atas perhatikan contoh berikut:
Misalkan garis
i. Jika
ii. Jika
Apakah transformasi T ini merupakan suatu isometri?
Penyelesaian:
Ambil dua titik sembarang
a. g sumbu dari
b. g sumbu dari
Perhatikan gambar berikut ini:

Kemudian pandang
a.
b.
Sekarang pandang
Karena
Contoh lain:
Asumsi bahwa sebuah sistem koordinat membangun suatu bidang datar dan pemetaan

Dengan rumus jarak diperoleh:
Karena itu,
2. Sifat-sifat Isometri
Suatu pencerminan atau refleksi pada sebuah garis
Teorema 1:
Setiap Isometri bersifat:
a. memetakan garis menjadi garis
b. mengawetkan besarnya sudut antara dua garis
c. mengawetkan kesejajaran dua garis
Bukti:
a. memetakan garis menjadi garis
Andaikan g sebuah garis dan T suatu isometri. Kita akan membuktikan bahwa
 |
Ambil
i. Bukti
Ambil
Sehingga
ii. Bukti
Ambil lagi
Bukti serupa berlaku untuk keadaan
Sehingga
b. mengawetkan besarnya sudut antara dua garis
Ambil sebuah


Andaikan
Sehingga suatu isometri mengawetkan besarnya sebuah sudut.
c. mengawetkan kesejajaran dua garis
 |
Kita harus memperlihatkan bahwa
Sehingga suatu isometri mengawetkan kesejajaran dua garis.
Akibat:
Salah satu akibat dari sifat (b) teorema 1 ialah bahwa jika dua buah garis misalkan a dan b dimana
Bukti:
Dipunyai
Artinya
Jadi apabila
Teorema 2:
Komposisi dua buah isometri adalah isometri
Bukti:
Ambil dua isometri, namakan dengan
Yaitu
Karena
Soal Latihan
1. Diketahui garis-garis s, t, u dan titik A,B seperti dapat dilihat pada gambar di bawah ini.

2. Diketahui garis
3. Diketahui lima garis g, g’, h, h’, dan k sehingga
4. Diketahui garis-garis g,h, dan h’ sehingga
a. Jika
b. Jika
c. Jika
5. Jika
Pembahasan
1.
Gambar:

2. Diketahui garis
Gambar:

Karena
Jadi, menurut teorema ”sebuah isometri memetakan garis menjadi garis”, dan
Titik
Titik
Jadi
Karena
Jadi
§ Koordinat titik
g : x + 2y = 1
h : x = -1
substitusikan x = -1 ke persamaan garis g : x + 2y = 1, diperoleh:
-1 + 2y – 1 = 0
2y = 2
y = 1
Jadi
§ Koordinat titik
Titik
Karena isometri maka
Jadi,
Misal titik
Absis titik
Diperoleh
Jadi,
Jadi, g’ melalui titik C(-1,1) dan
Persamaan garis g’:
Jadi,
3. Diketahui
Andaikan g tidak sejajar h, maka menurut teorema, bahwa isometri
4. Diketahui garis-garis
a. Jika

Jadi benar jika
b. Jika
 |
Jadi benar jika
c. Jika
 |
Jadi benar jika
5. Jika g = {(x,y) | y = -x} dan h = {(x,y) |3y = x + 3}
Gambar:

Karena
Menurut teorema, “ Sebuah isometri memetakan garis menjadi garis ”, dan
Titik
Jadi,
Karena
Jadi h’ akan melalui titik
Ambil titik A(0,1) dan B(-3,0) karena
Jadi
Persamaan garis h’:
Jadi persamaan garis
II.2. Isometri Langsung Dan Isometri Lawan
Untuk lebih memahami isometri langsung dan isometri lawan terlebih dahulu kita bahas fenomena isometri yang diperlihatkan pada gambar berikut .

Pada gambar 1 tampak bahwa apabila pada segitiga ABC yang dicerminkan pada garis g dimana, urutan kelilingnya A→B→C adalah berlawanan dengan putaran jarum jam menghasilkan peta yaitu segitiga
Pada gambar 2 dapat dilihat lihat sebagai isometri yaitu suatu rotasi (putaran) segitiga ABC yang mengelilingi titik O. Dimana, pada segitiga ABC urutan keliling adalah A→B→C adalah berlawanan dengan putaran jarum jam dirotasikan mengelilingi titik O yang menghasilkan peta yaitu segitiga
Untuk membahas lebih lanjut fenomena isometri di atas, kita gunakan konsep tiga titik yang tak segaris. Andaikan (P1,P2,P3) tiga titik yang tak segaris maka melalui P1,P2 dan P3 ada tepat satu lingkaran l, kita dapat mengelilingi l berawal misalnya dari P1 kemudian sampai di P2 , P3 dan akhirnya kembali ke P1. Apabila arah keliling ini sesuai dengan putaran jarum jam maka dikatakan bahwa tiga titik (P1,P2,P3) memiliki orientasi yang sesuai dengan putaran jarum jam (orientasi yang negatif), apabila arah keliling itu berlawanan dengan putaran jarum jam maka dikatakan bahwa tiga titik (P1,P2,P3) memiliki orientasi yang berlawanan denga putaran jarum jam (orientasi yang positif), jadi pada gambar 1, (A,B,C) memiliki orientasi positif sedangkan (A1,B1,C1)memiliki orientasi yang negatif, pada gambar 2 orientasi (A,B,C) adalah positif dan orientasi (A2,B2,C2) tetap positif, jadi pencerminan pada gambar 1 mengubah orientasi sedangkan putaran pada gambar 2 mengawetkan orientasi.
Definisi:
1. Suatu transformasi T mengawetkan suatu orientasi apabila untuk setiap tiga titik tak segaris (
2. Suatu transformasi T membalik suatu orientasi apabila untuk setiap tiga titik yang tak segaris (
Definisi:
Suatu transformasi dinamakan langsung apabila trasformasi tersebut mengawetkan orientasi, suatu transformasi disebut transformasi lawan apabila transformasi tersebut mengubah orientasi.
Salah satu sifat penting dalam geometri transformasi adalah:
Teorema 3:
Setiap refleksi pada garis adalah isometri lawan.
Teorema 4 tanpa bukti, tidak setiap isometri adalah isometri lawan. Hal ini dapat dilihat pada gambar 2, dimana isometri (yaitu rotasi pada titik O) adalah sebuah isometri langsung. Oleh karena itu dapat kita kemukakan teorema berikut, tanpa bukti yaitu :
Teorema 4 :
Setiap isometri adalah sebuah isometri langsung atau sebuah isometri lawan.
Soal Latihan :
1. Pada gambar berikut, terdapat tiga titik tak segaris yaitu
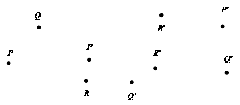
2. Isometri

3. Sebuah isometri
 |
4. Diketahui garis-garis

Diketahui pula bahwa
a. Lukislah
b. Bandingkan jarak
Pembahasan:
1.
![clip_image010[10] clip_image010[10]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjhr7oBXw2V6S9fWjPytE_-kHF5oNgdiqChe9hhgzAgsa2PmyzuM1GzklTahLUJtea5-bhb2Hbg1SpMnE1rQFKUqzCxzV2SwCqmrrtpmwk_L5ag1OXfrmpcMbx9tfGvxqrLisW_iAz_Ok0Y/?imgmax=800) |
2. Karena
 |
3. Karena
 |
4. a. Gambar:

b. Karena
Maka jarak
Jarak
Jadi jarak
Karena jarak
Post a Comment for "ISOMETRI"
Terima kasih atas komentar yang telah anda berikan