LOGARITMA
1. Pengertian Logaritma
Logaritma adalah fungsi invers dari eksponen (perpangkatan). Secara umum:
Dengan:
 dibaca logaritma
dibaca logaritma ![clip_image011[1] clip_image011[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgKbzBkJdSVWKH0lxSQHk0RM348496WCiIzut2iOse4ARqhioaR4NUuZOBMWfZZMtyUEPyUgG8yYj3DJ9y_dvBUaeCEk450SpZvdB7rWYkX9eGgXzDXg3CmyRZzEtcIGI6aJ6MZ7y4WrV0w/?imgmax=800) dengan bilangan pokok
dengan bilangan pokok ![clip_image005[1] clip_image005[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg2Hz_BkFHcPkzyQIOH8CFJqKdwBXSTk47h0nr7Fnok3Tj6YRrRjyivRBX9QviRT-SwtNpyr_65YMzPxoX2dpmbjDQ3xmqzSaeNJCNEx_5DS7Ot6P1Ak_I6UUZiPubvznFc3rGYopBD8_PX/?imgmax=800) . Apabila basisnya 10 pada umumnya tidak ditulis misalnya
. Apabila basisnya 10 pada umumnya tidak ditulis misalnya  sama artinya dengan
sama artinya dengan 
Contoh :


2. Sifat-sifat Logaritma
Untuk nilai![clip_image007[1] clip_image007[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhe2nJE1W5uaT_GvY0JAx417A3UFw9uYcdEh9neKSvAlD6UqFIapW3KL5FokZEfMq9KwszZZbLDrS_AQaTNkSJe1EAYFBp1ASX7Zie6DmJ9ZTWcee2eafE-YvpBuGjP9zhjGqEzPjmfNuff/?imgmax=800) ,
, ![clip_image009[1] clip_image009[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiouz86S0DGQSLLzjDju-Pu3mk7b52U0-5H678tl-StmmgFT6-iuEgIvvqBBssrPMz_xmaxdkFDdKf_I9NV7b1TfE5FTDyAtu9w0qEQWofrPx3_o2EvzMQeDSfPNB_sAwqz0uMnPIzImbDd/?imgmax=800) dan b,
dan b,![clip_image013[1] clip_image013[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhmDVjGTvlq4kbOWapuvInFRL0ae3vEeQd9BBAWrdF2UurAhN_Uxm2uoeS7pTP8xtVnqSHnlncqsP15V_hj0YQVioE72VNGdqFUktScz05rJIT0v9dNuwS1G6xiW9Z7tZmrMlW8rZbOt1sD/?imgmax=800) serta
serta  dalam logaritma berlaku:
dalam logaritma berlaku:
a.
b.
c.
d.
e.
f. , dengan
, dengan 
g.
h.
i.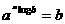
j.
Contoh:
1.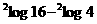 = .....
= .....
Jawab:
![clip_image054[1] clip_image054[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcdAP2OzHDV_XgnrR9bUW70G0F9-FWCQcC3CGub8F7vL1PENuPNC8_HNK9T5nX283vfyZLrAbDdzouI0KzPs36gBdNSMt6cXKq7Vl-A5L3YCKabGptuhoEUFKf37gztQaYhuTe55q0hutc/?imgmax=800) =
= 
Jawab:
log 36 = log 2 2
2![clip_image060[1] clip_image060[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhcbyvljoCVbb1j5-WimLMgEQPLoMwDCydMX4o0GaaIm5UYxP-QQtmDnvJV__JrerKsC5j0_ITb3WxRAXmACs1WXkjIRGY3u2EymP45ZgZ5IvRt5EUDXGmsfpA-eeROMvsXXU8GjUJH9Viz/?imgmax=800) 3
3![clip_image060[2] clip_image060[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhOJDzUD1MgaYL9zUMHf5loWROLLGPEt6tX1hwpo1j8vuMjB5KrONGL6ukzXmOfat29b6fbYEJEs2-qtIN5a1LjcmgtejaPbMgDCqsIAsa3ipqhAQo_O70D1KL79UsZyZilwTpnuPrUVk-G/?imgmax=800) 3
3

Jawab:

a. Menentukan logaritma antara 1 sampai 10 dengan menggunakan Tabel
Pada tabel logaritma kita hanya dapat menentukan nilai logaritma dengan bilangan pokok 10, sedangkan untuk bilangan pokok yang lain perhitungannya dibantu dengan menggunakan sifat sifat logaritma.
Contoh: log 1,12 = 0,049 dan log 2,01 = 0.303

b. Menentukan logaritma bilangan lebih dari 10 dan antara 1 sampai 10
Sebagai dasar untuk petrhitungan adalah terlebih dahulu mengubah bilangan yang diketahui ke bentuk baku.
Kemudian menerapkannya ke dalam sifat perkalian logaritma.
Contoh:
log 200 = log 2![clip_image060[3] clip_image060[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiY4_yEoagMerG5C2PkeNOjC_FzRN_3aAwvKzGmBWDJI648lCGe8fP2HwzzURicxcG3szNe2BuIc1a5_-r5doSEXLtIDW-6mMQA6fTz6EIxMF-Fz6VOgANs5mx8JD2cfTHJNIB26XBwy8to/?imgmax=800) 100
100
log 0,0025 = log
Logaritma adalah fungsi invers dari eksponen (perpangkatan). Secara umum:
 |
Dengan:
disebut bilangan pokok atau basis,
dan
disebut numerus (bilangan yang dicari logaritmanya),
disebut hasil logaritma
Contoh :
2. Sifat-sifat Logaritma
Untuk nilai
a.
b.
c.
d.
e.
f.
g.
h.
i.
j.
Contoh:
1.
Jawab:
=
= 22. Jika log 2 = 0,301 dan log 3 = 0,477. tentukan log 36
Jawab:
log 36 = log 2
= log 2 + log 2 + log 3 + log 3
= 0,301 + 0,301 + 0,477 + 0,477
= 1,5563. Sederhanakan bentuk
Jawab:
=
=3. Menentukan Nilai Logaritma
a. Menentukan logaritma antara 1 sampai 10 dengan menggunakan Tabel
Pada tabel logaritma kita hanya dapat menentukan nilai logaritma dengan bilangan pokok 10, sedangkan untuk bilangan pokok yang lain perhitungannya dibantu dengan menggunakan sifat sifat logaritma.
Contoh: log 1,12 = 0,049 dan log 2,01 = 0.303
Tabel Logaritma

b. Menentukan logaritma bilangan lebih dari 10 dan antara 1 sampai 10
Sebagai dasar untuk petrhitungan adalah terlebih dahulu mengubah bilangan yang diketahui ke bentuk baku.
Kemudian menerapkannya ke dalam sifat perkalian logaritma.
Contoh:
- Jika log 2 dalam tabel adalah 0,301. Tentukan log 200!
log 200 = log 2
= log 2 + log 100
= 0,301 + 2
= 2,301
- Diketahui log 2,5 = 0,398. Tentukan log 0,0025!
log 0,0025 = log
= log 2,5 - log 1000
= 0,398 – 3Semoga bermanfaat :)
= -2,602
Post a Comment for "LOGARITMA"
Terima kasih atas komentar yang telah anda berikan