Penerapan Fungsi Eksponen Dalam Bidang Ekonomi
Fungsi pertumbuhan merupakan salah satu contoh aplikasi fungsi eksponen dalam bidang ekonomi. Sifat utama fungsi ini adalah meningkat secara monoton. Fungsi pertumbuhan mempunyai beberapa bentuk, dengan atau tanpa asimtut yang merupakan batas atas.
Dalam karya tulis ini fungsi pertumbuhan yang dimaksud hanya terbatas pada fungsi bunga majemuk, pertumbuhan penduduk atau biologis, kurva (fungsi) Gompertz, dan kurva (fungsi) pengajaran.
1. Fungsi Bunga Majemuk
Besarnya modal yang dibungakan tergantung dari waktu lamanya modal dibungakan asal tingkat bunga konstan. Jika modal (pokok) sebesar![clip_image002[4] clip_image002[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh9zM1XL7i2o3Mn32Mlulmvm1V6TU1wkGYXaWeILAhYKUaji0yUxOiVqKUrnN43JARitoAnEgBAbQ7WDRYLCiNKZxnKedCvPrqb-zYQl-W2TzUc-7Lb-PraS57RZYIrH8Lkayrp3m-x8Uw8/?imgmax=800) dibungakan
dibungakan  kali per tahun dengan bunga sebesar 100
kali per tahun dengan bunga sebesar 100 % (atau r) per tahun maka setelah
% (atau r) per tahun maka setelah  tahun, modal tersebut akan menjadi:
tahun, modal tersebut akan menjadi:
Apabila![clip_image004[1] clip_image004[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjdfzvfSm8N4GEp21ztDxUV3uW9tryUZiqg6RT7RqMDCYJqOneMFk4poEKT3fXce_ipaQsEHQsv8-aesVsVSg_Dmj0O7GaI79G66KopgU378nblNlMyKUv7acW1p5v4f7nPZM_Kym-o9wLi/?imgmax=800) sangat besar yaitu
sangat besar yaitu  , maksudnya bunga yang dibayarkan secara kontinyu atau bunga ditambahkan terus menerus terhadap modal, maka persamaannya akan menjadi:
, maksudnya bunga yang dibayarkan secara kontinyu atau bunga ditambahkan terus menerus terhadap modal, maka persamaannya akan menjadi:
Dengan,
![clip_image002[5] clip_image002[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjHuG8z_t_2mJNqM9jwZWfrvldqnFs59ULYttKyXibP9_oJVkw5v6t5uGISiqlJb6TbAFAtweEtjBxQZdwcbrPeuuJUfPnqVAKM3oQEkQ23b87_ort2izVI0BdItEHs63qWzl15LgjeE1rC/?imgmax=800) = Modal awal atau besar modal pada tahu yang ke nol.
= Modal awal atau besar modal pada tahu yang ke nol.
 = Modal akhir atau besar modal pada tahun yang ke
= Modal akhir atau besar modal pada tahun yang ke ![clip_image008[1] clip_image008[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgudzEq0FjTF1CpI3rHBvS8x0HLyIxxjAReLfyNLh5WDtas8_5LaH-fHxDCabCh4VTTF0kl8lwEyUEh95bZDO_TM6kkmM0QZdN3-mFvkZooR9UiRSUiW7CU6tQ0LpIyyZtwOUbD8IWVRJiw/?imgmax=800)
 = Bilangan basis dalam logaritma natural
= Bilangan basis dalam logaritma natural 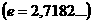
![clip_image004[2] clip_image004[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjROhKDY6Hrqbuccq9gpD_wWvwdP8WlyF1JdKipw6TDW7OGb473GnkUuIuomVHI4dyOUZV4Bve8a70NApVrnttqQGS25iVkUrXv4j6O8cftYXMlp8Olqd78yHNa9M6hO_A2SEhwy9eopIHT/?imgmax=800) = Kelipatan bunga yang dibayar per tahun
= Kelipatan bunga yang dibayar per tahun
![clip_image008[2] clip_image008[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjG4hlvlqSWnbHaGq0W_L4n1jYlY-PUuDQb_xdkb9bQYDAj8h8AqIGH8YBUirs5wph6BC0Rv-BJ7lzzL5_o2bt-WB2s5PeIc6w27gb4GdMkaA5OCv3tXcKCE2ZucAdPW5nliTe7k675psp3/?imgmax=800) = Waktu lamanya modal (pokok) dibungakan
= Waktu lamanya modal (pokok) dibungakan
![clip_image006[1] clip_image006[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg0nc9YJaOWMjHgw3yvpwrP0YG0g5dUdyAW7MhppbTEV8jN5AiBB1L1b0CulOa8Mk2C6KI61_zS-g8WFyfaSNHkOlBgIkjgepG7bAOE9PhZEn1MlDR-_SHoCbZWnaTlgRPz8_LcLX4JvZ-o/?imgmax=800) = Besarnya bunga per tahun
= Besarnya bunga per tahun
Jikan fungsi![clip_image014[1] clip_image014[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiSoZh-_BOxuMWHYwBX5aL0FqgO9owA8j47Ik4USFFOrN5c_X9upRazoU8HwsI177rOBa6-WGiSbcU_Uye4-Sy5NyHsdU0MM3fRYV0mB-64WJLbYispHT0ikkdRsZYPjOiBnq1PdTq11rL-/?imgmax=800) dibuat grafiknya, secara umum bentuknya sebagai berikut:
dibuat grafiknya, secara umum bentuknya sebagai berikut:
Gambar 02 Grafik Fungsi Bunga Majemuk Dengan![clip_image012[1] clip_image012[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjl3z5pTs_qU0GPp1dFEvuOOFJ2UBlav_XJK7WL4o2wuBOKRuD5AAy7_s0tHGrojInICSgE1R-yG_3FJ3NbBBsOhbjTkmNj57Cub1GEBlX7fLS6bju_XhvEvfzVIl0w7vXP7t6h1kmpx6Yi/?imgmax=800)
Contoh:
Seorang petani membutuhkan uang sebesar 5 juta rupiah pada 10 tahun yang akan datang. Berapa jumlah uang yang harus ditabung mulai sekarang dengan bunga 24% per tahun untuk memperoleh jumlah uang yang diharapkan?
Penyelesaian:
Diketahui:![clip_image016[1] clip_image016[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhyhAXghyphenhyphenZdTithoUUXebzfcQZI-cn_a3e8gi_QXSrp59jGOR-m73_L6os9_EjcIT7ks9eGpjFG6wDe_syXwa-wDfNhyphenhyphensdruv8QTOfQTkY-xDqWpFlXK7-OxnvYbhdqqBl3Z06k8HTesA39/?imgmax=800) = 5000000
= 5000000
![clip_image008[3] clip_image008[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg_7XTEe9i3VQgfpwp_1cOVVmKOv1QLW6D-7Gwa8K1O5fEFCNVbpaC1XxhREjR1koIXEwsMr0BxqpVC2dSbDYQuQ5aIvZ1pb4mBtsta50elyeLnxaTEZPkLHOx_m5UA10yr-rctEz4S0Sdy/?imgmax=800) = 10 tahun
= 10 tahun
![clip_image006[2] clip_image006[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg2PstialR-nPGowb0NNHVSTf_TxjEg91VWk-1BXvtkA8AZnUXhNMJnNUrT1glXqAFi2jIRFn-T-v-_1k4mrPQnkMT021ZrN7fWECIAKoIBrgrqh8BUdtZ8OxcHMk14L1LQOeII_vvRHKd4/?imgmax=800) = 24 % = 0,24
= 24 % = 0,24
![clip_image004[3] clip_image004[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjl8YNfi2HE9u8t4eDbj3G80uQSfFgi-9rkfMpXnDuNxK12kvrEI7Ozd8EiC4jhAMskkjRe-ZGHKwRyKCyjEkFSYrXcC548b0Mrf_x1B0uW4RirukussPpozFebGCncCkiqdXxbMgcm56eN/?imgmax=800) = 1
= 1
Ditanyakan:![clip_image002[6] clip_image002[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhp95JbMmrHH-gzNDD26shmO975pkMMXIjEqyUlljZ7JSlwriF56iuJZbbAAKuP0aTkihkR3YhbULVG1-wwXZW_zZwsxninyYuIvLEfEV4dRW-QUjTN1H4rmoy6x6sLQ4CvkYtTcCTSyeC_/?imgmax=800) = ...?
= ...?
Jawab:
![clip_image010[1] clip_image010[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgZl9c8nOxW97U2rK623OLPL0BZEkEqXpm4KSVz3dVzSJBDwpW_0OD-3CoPadafYb1_WGZyr2kQAhYlUyUaJmIRNRn4uOtodVBQFVuuUmo793VwwCHPDLVtfc-zRiX_DPoAVr2-TuMajCb5/?imgmax=800)




Jadi, uang yang harus ditabung mulai sekarang sebesar Rp. 581772,49
2. Pertumbuhan Penduduk
Bila penduduk suatu negara (daerah) pada suatu saat mengalami pertumbuhan sebesar 100
mengalami pertumbuhan sebesar 100![clip_image006[3] clip_image006[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhDaZfq7Cn3ehddg528K0njarKa5QvnX5dFJvx7sParaBrogEaljrfDUi3EVGLy6brIn-mpjjS1bSwAsDWklOOGu8RroTlJsoc4bas1ri_K3s31CJbTdcwmwuenuuxAsAdVMs06XNr2xIH_/?imgmax=800) % per tahun (atau
% per tahun (atau ![clip_image006[4] clip_image006[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjgC4jkFtTMED99R9KQn73u-dKeL1PK1hymjkBRY2KvQVnq7owWRdMb7sU98loXDMzmJnB2SHVF9f4Y9DUA1EWX56KjPQQP7IsVK7YnPurvgJ8Bag-smeNfyuwjzag36YHFNe8BQLJ5rENh/?imgmax=800) per tahun), maka setelah t tahun, jumlah penduduk menjadi:
per tahun), maka setelah t tahun, jumlah penduduk menjadi:
Bila suatu negara (daerah) dengan jumlah penduduk yang besar, maka pertumbuhan penduduk berlangsung hampir kontinyu, jumlah penduduk setelah t tahun menjadi:
Misalkan pada persamaan
pada persamaan ![clip_image040[1] clip_image040[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiIC4_fmeiLmhhI4JI_kN6NFniH-nydk5wc7hKnocIEBMofO75PSNI0q8JagF1fHJEqwcNeYCJtlbm63ycf3fuJ8Pfv8QRfC3Nsw9yGC0y8ohoVXzSH-tOeArrEEKl_5Oiq6t2oX5KYzu1Q/?imgmax=800) sama dengan
sama dengan  yaitu
yaitu  , maka persamaan di atas dapat dinyatakan sebagai berikut.
, maka persamaan di atas dapat dinyatakan sebagai berikut.
 = jumlah penduduk pada tahun yang ke t
= jumlah penduduk pada tahun yang ke t
![clip_image036[1] clip_image036[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhOO18RYarSe2Y1Ss9_giWtZvzYqPV5V5msGiSRXnGrlvwo3vgbiemsRcvTd7nHEaXbV3SiliICMYTlc74WJ0yUFsAY9mnz21PNl3F3vZfrXBNsMJz6CpZKctxKWtxY-rEti0p2AhMQoPN7/?imgmax=800) = jumlah penduduk pada tahun awal yaitu tahun yang ke nol
= jumlah penduduk pada tahun awal yaitu tahun yang ke nol
![clip_image006[5] clip_image006[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj5YcLcPGDOf3w6L-3V_Ax5tzeQC84WUGVqPn-bUKR8SizRWbPi1v2FKdwl5AcGq5-yVitVatS2mzqiZ7I9yjWeQ4Exo1pWuG4DVhLQgLWVaB3D_LNVMbZe3UmDFRSW4xa4fKtb8ikdZDP9/?imgmax=800) = tingkat pertumbuhan
= tingkat pertumbuhan
![clip_image046[1] clip_image046[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhg7Hm_TsqZk-eszVbAKWuHyQd9P3uoHC3Ssg_e4rx55Shfy_WpMy_SG6HY7A3SaMHX2qW_N9IoDUrNPzyHJ-l_F7CabC6IwoF9K5jA-zKdIT9KFP19oXUlTxfXlPt0EoPbpJHBM3A2DsBF/?imgmax=800) =
= ![clip_image044[1] clip_image044[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhNFf32xpdD3vcJPQ0JsGsdgYX7TW65RtEG4KN1ZJ1BI5OSs0TXQ_WwwpTHsWTEuxWmHleTccd99lSIshEhSOzYIKeZzYJfOHxsci7ZgqhO9TFgzFDCPxriNtAgZu2ZCc14pUzuize-N6pX/?imgmax=800) = tingkat pertumbuhan ditambah 1
= tingkat pertumbuhan ditambah 1
Contoh:
Pada tahun 2001 penduduk sebuah kota adalah 629039 jiwa. Sedangkan pada tahun 2006 jumlah penduduknya adalah 771186 jiwa.
a. Berapa tingkat pertumbuhan penduduk kota tersebut?
b. Perkirakan jumlah penduduk kota tersebut pada tahun 2016!
Penyelesaian:
Diketahui:
![clip_image036[2] clip_image036[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjUg-fDOt-hBTaVq6pU6T-11LJFnaRiWh2DchdtAGJ2KLUhkBQfaTM1JQXORwPSi79tX-idXHvgpAfgrjoGMUftmWEApsL3MD3wYo__FWxuKUfB3Mv1C-l7B3XV9W2so8BZoDa6f8As38kN/?imgmax=800) = 629039
= 629039
![clip_image052[1] clip_image052[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhGL_SeEsA5myrCU4fbMKWW9I9IJa2iBt9stXeM0co5CzW557lzqMc7o6XDlYnKdUdOxurJPXzI7K7qlCU698s1_dX0FQ1Fab2dKsMBWAHPXdkQxPjtpcFBRUhlel1B72_GB2nOXWiFvY2g/?imgmax=800) = 771186 (tahun 2006)
= 771186 (tahun 2006)
t = 5 (dari 2001 sampai dengan 2006)
Ditanyakan:
a.![clip_image006[6] clip_image006[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjKfdrOpIJxVTQD0iQvvxhJy-AkESlQlQ-MehDAfrYXLC_QQ5EWAYwCQonBXoJWcfJ_QTggBgy3T7eIBM1EZW4hcRxi8-8Hd2N3u6oNk53jrXqhWKPSJnKnUPWBTeOZxZMPIIEJ8DgQXMFu/?imgmax=800) = ...?
= ...?
b.![clip_image052[2] clip_image052[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhVCLTvioRO-BXKD6CJ1MVh_3VemnFAKpA0XnwRMHzoV7tOLqt_8HL4sRF7znneFCJP7DJI5j_XyQ9-wH0i65TdjJfPJXGoznsPglOF-gldKaWRDGokGk2-jwjK13JHU2TJxQYCOj1TxJ_e/?imgmax=800) = ...? (tahun 2016)
= ...? (tahun 2016)
Jawab:
a.![clip_image040[2] clip_image040[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEheXuwSkH6s7upReboM8PL6M-Q_vHfR_2zUW_Q6DuEnkNxRHziSU3Y96bi7hmxDWlytM_OQIXLquK2fB5a06pJwVtyNLMSV-uegcNU1Jwg8rehy8QhMnfN3pdhc6irla2E_BKAGdJ0ucBFm/?imgmax=800)








b. t = 15 (dari 2001 sampai dengan 2016)
Karena t cukup besar maka untuk mempermudah perhitungan kita gunakan logaritma, sehingga:











![clip_image059[1] clip_image059[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhyXdxXbd4_pERhpujOlRTH_zPawL0_2Dp64Ux1fWMONEC_5WEUa_D2A_-CCdexZiF9WXuXQCpbAWjFqvJU5Kx839qeIpXuw0GcBroENEz3JtU-EKSn259LSZ6akpILkJoNHxR6ZOPyiKvB/?imgmax=800)
![clip_image061[1] clip_image061[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiUrEvCJxNpUW3egOLqkorWpI21myTymVerGZ0CijLyY5Bgcz8WA3SiNMmD4H_FQM1TPJgFsT4bUxNcnUC-UfwJXvdU9SH_fHZEElODNvOtLB-pGva6eWKWQYnX69hUgWwkY6VXbakjDlEC/?imgmax=800)
![clip_image063[1] clip_image063[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiKVPvTzAIeAZP86K44q1SN1TCJ_dSJf1VjJKSANzDeYLt8IaZdAfnft9FUypEBGpfgegyV2mhblNy5cu9OHA9OpxvGI60s1w52puSc-b8ZzDIyAgnG1Kvmz4WOokr1jv6Blp-4N6ZRUyJE/?imgmax=800)
![clip_image065[1] clip_image065[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgyWGr_ga2_pPlS_Eynci6TGh2CIFqxrcY4sUYVmx4G7Bb2MC-nQ2Qs364_rnd6ZLSsYZng_vhniLHKfXKalmgihEDblGmG49XgNu9uAxUrzC4Fg0K_CK1d5qMEsfBbjV2z_MNK43_pOs6Z/?imgmax=800)
![clip_image067[1] clip_image067[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhFByq584GhOEC94dLzT-dbxGhL-25cylnBtPrOEFz4KwUZBhNBdVcJEwvmsFncXlR5U5y8xNpsVtMeNf4E0yVzSIv2RnTG5vS01VBbwT62PyLMLhj1nlq7a5ZxdiIVgnVgZXO7XkppXp1F/?imgmax=800)
![clip_image069[1] clip_image069[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhBNiy1bO0QTLhhBNh-98ttcLvHllZn_MXRBGPrtDSjjKDlLeUYwCI-BwmXHv_9H3-yvXbCeKRnYXIhbZBHW-211PE8c05kTRKu4h_DMGUFWZwGH85b1uzBM9_31NACx8KMr0uXIUzE8s90/?imgmax=800)
![clip_image071[1] clip_image071[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgYzqz1HilTsW53Atmt9eD0BzkIkDccKhX9qYFEOKjIEEV7OysANZc7IazGhUqLDlrBTPvz-dhKw3KQigk86hI2F04GRnTwmPSv-tANYPOOKjdJDbCwqdrIFXZ1kuN8etu4LzP3MRSgMcQh/?imgmax=800)
3. Fungsi Gompertz
Fungsi ini menggambarkan perkembangan yang lambat waktu mulai tumbuh, dan waktu mendekati asimtut batas pertumbuhan. Fungsi ini dinyatakan sebagai berikut.
Keterangan:
 = jumlah penduduk pada tahun ke
= jumlah penduduk pada tahun ke 
![clip_image046[2] clip_image046[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj2inkypj2PfMqKtY30fD2oT5_cxFrbEcyYl-_VcUls3952cXqHo56ZhUQFcVtWZdoug51LGM-bn_ZW-GrToUYczypE80DR0afRTHowo_EU2nLAiw8ib61FM0EScpL9_8RhEwyCib13jiYm/?imgmax=800) = tingkat pertumbuhan (dengan
= tingkat pertumbuhan (dengan  )
)
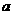 = proporsi pertumbuhan awal
= proporsi pertumbuhan awal
 = tingkat pertumbuhan dewasa (yaitu asimtut tertinggi)
= tingkat pertumbuhan dewasa (yaitu asimtut tertinggi)
![clip_image099[1] clip_image099[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiIDfTcjNzdjDZGWJXLR3X8-eNG1DMM8LQnaGM1RvUt4lMX6-1FEgSoAi7k4YPGm1S44p3OpF134dfxQFJIt-rlZdpH5lMEHm2-tp4k4nPvmfaSRZQLLFBave9roZEF0kXIL-YK2sxP97KH/?imgmax=800) = indeks waktu
= indeks waktu
Sifat utama dari fungsi Gompertz digambarkan dengan dua jenis kurva di bawah ini.
Tipe I:
Tipe II:
Gambar 03 Kurva Gompertz
Kurva I, untuk nilai![clip_image099[2] clip_image099[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjjSyHqvT-Y3bpZgK50cgkWBmZI1gDNOQbxiVvM2PVYOn0iNLFsXFIthwUYAWeW5YVKaVET5qsGeXAQ4dJL0noJPQXo2z3q8IzQUnpZxm6IB1Debc3Eq1oBuvrvkl4fUmEkKdmZkTAXneia/?imgmax=800) kecil yang positif kurva cembung tehadap sumbu t (berakselerasi positif) dan untuk nilai
kecil yang positif kurva cembung tehadap sumbu t (berakselerasi positif) dan untuk nilai ![clip_image099[3] clip_image099[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEj87niVafqkqsAAc5xxRJIb2TDAtqwp0IRsuORdCtukx1na8hbI5TNR0q90bnSxlh3ZwZo1wuc35bDljnECEN27eEuM3vTje2Ln1GhrsId5I-0l5fYYhKT4p1IZChtJCA3QNDm9nKgsZlgZ/?imgmax=800) besar yang positif, kurva cekung tehadap sumbu
besar yang positif, kurva cekung tehadap sumbu ![clip_image099[4] clip_image099[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhD3m4gE0fl3K1Ur7nxKLsvntbtRMRkbKeAXXDYaO91ezuTU97NFzzc26ZSzUE7T9eJkbFXNgGAUCDNmWtgATJ2w29ebKDWaJjUQ1pDprYqKlxUKQpS_cE8Yh0Ps3b-XlLtJCEyQwPUoi-s/?imgmax=800) (berakselerasi negatif). Sedangkan kurva II, untuk semua nilai
(berakselerasi negatif). Sedangkan kurva II, untuk semua nilai ![clip_image099[5] clip_image099[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjYxxNHPejbKSfT1neMf1-kFIQwA6VrUKzTgxSJInkwtdz1klUS6c0c5CviSQA2umx3FwByjwMTgE6FMVrgRvJNePgJXL2JbpizNbFi0UcP-iyKNST4B5p0duw4yY1rQnDPKTWt1-Wlz-Gi/?imgmax=800) positif, kurva cekung terhadap sumbu
positif, kurva cekung terhadap sumbu ![clip_image099[6] clip_image099[6]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjnUJkwwJ_Z6evj1z845jG37e7Qsg4GBlrikokSbyIkOwrTtAdKdR3PG7UGXKcuPxyMvKzNUWYfe7IDhNqEmVLOi27WtxQ7_JuSIGiJUJatpQwIpsR4MiVz56eIoZtMReY_CUt55mUPcy7G/?imgmax=800) (berakselerasi negatif).
(berakselerasi negatif).
Kurva yang ditemukan Gompertz ini dalam bidang ekonomi digunakan untuk fungsi pendapatan total dan produksi.
Contoh:
Penjualan setiap bulan dari sebuah perusahaan memenuhi fungsi


p adalah jumlah pengeluaran untuk promosi dan advertensi. adalah penjumlahan atau omzet setiap bulan.
adalah penjumlahan atau omzet setiap bulan.
a. Berapa besar penjualan bila pengeluaran untuk promosi dan advertensi sama dengan nol atau berapa besar penjualan awalnya?
b. Berapa penjualan maksimumnya?
c. Berapa besar penjualannya bila pengeluaran untukpromosi dan avertensi 5?
Penyelesaian:
Diketahui:![clip_image116[1] clip_image116[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgeNsJEn65s2BhfKnalSxRnhL0tv-yjY5Wui6690zSdEajDHFNyM16PHn5qH9eVtIm34z52aEy77M6ucBJFo7HrOIZ-wf920JCUtlt8O4-_ix3_eT69JZVIGCSRtFrxXEuUC9dm3oEW6zkb/?imgmax=800)

Ditanyakan:
a. jika
jika 
b.![clip_image118[1] clip_image118[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEieBM6piAbM5Rvjc1rBOJIFFm10LIHzGIJI02Q_pkbncG_AW0h19OKpw1yyB2ZYqErNdFhqexoEouMMiRcywNSDI9AnVPrsWEfR1A1z1SAunVibWQWq11xbWmTs0TE8RMOW4OX9nKMzwB4u/?imgmax=800) maksimum =.....? (
maksimum =.....? ( )
)
c.![clip_image122[1] clip_image122[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgiQk2JRrkoHgFYmutw4cTTLoRkFtySo-7zINoeuUYL_EGK_xutjAFXyPgg8LdpbLwa86nw18I_WYgqEKzaqG-urmTsz3tpjvGrqrYDjF9KYTFgibVk11pK0j07_z9bZw5jf1JLl07PV_US/?imgmax=800) jika
jika 
Jawab:
a. Jika![clip_image124[1] clip_image124[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhg9d6ufQzQvXv-zYlIUlJ7w6SuHyjLtSJv1M4oIYIhAuo9I99ooRcx8ILCFatQaj6YNPkplLvcEbyiSDKUhrFXhLgriSNqw_BYNn6U_UqtBn2IpEjlgJ2T19ysvibdRg5X0cp-5LRwRFcA/?imgmax=800) , maka
, maka ![clip_image118[2] clip_image118[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiFzZHuUPS87_v2m48LRvFKkV9KWSLhnsXB2DOflksd4sb1hq05OL6SKANYGuSf99pZUEethUwPmzJikEAl2T7WOTc3Yq7zJ-DI3Fbf4t632LoaAdMyxK0z6N4Zh-q309BOOhnSr531l49u/?imgmax=800) adalah:
adalah:
![clip_image116[2] clip_image116[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi-w7RILb_cxYiiUp-FwKum2W2Hy0NRDPN7-1WotQgBQoOTpo8cQVTtNsr8KUUUXBqnQea5mMDYw0ym_dgukQKb6SkT0fqAcDRmyMo5sf35XSJsM3qXoTf8Yj8tJZM_ceWrfaxqh0bKoj7H/?imgmax=800)



Jadi penjualan awalnya adalah 100
b. Penjualan maksimum terjadi saat tingkat pertumbuhannya nol



Jadi, penjualan maksimunya adalah 1000
c. Jika![clip_image129[1] clip_image129[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi1JzImvcHjeuESgt1dKWS2LBeXnWLaOtsfRecqmHQoE0_6HSysrR6XKkLWeKWnIXoZEtK6FAwPD75T12uvp20rN5h2D20eGxrzzuDh_jLQWJ-xa8WRY5O_s9jR1KKr8K0C2CD5UOoXB6ge/?imgmax=800) , maka
, maka ![clip_image118[3] clip_image118[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjEYUeJWcEgYqOJ3kFZZ93Gq0TvPRFh3iUosrgnSqa8ei1j9s09oofGeDV5iYc2XisFI0ke-GwCkxD1spPhtsGhC01h2XjLh5xt33tMuUKglWfVYAQ7WFNKaejCUYfZRZMuwaUNEsddtmAW/?imgmax=800) adalah:
adalah:
![clip_image116[3] clip_image116[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhzDDfMhwfQcq65LJgj2e-JcnzMTXeeo4MoeYB52DxrDmXKCkRbibYx7RT0lsmTBc7wVX6LKIrlftX5ScI_uCGJ-y9ri-Hqzv_vBcDPxVI4D-YfOGMNHgUbngDQsnRLDKm21Fic95AJ-aXe/?imgmax=800)




Jadi, besar penjualannya bila pengeluaran untuk promosi dan advertensi 5 adalah
4. Fungsi Pengajaran
Fungsi pengajaran umumnya dipakai oleh psikolog untuk menggambarkan taraf pertumbuhan pendidikan manusia, yang sifatnya meningkat cepat pada awalnya dan semakin lambat ketika mendekati asimtut batas pertumbuhan. Fungsi ini dinyatakan sebagai berikut.

![clip_image106[1] clip_image106[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgTm2hJ6VWw2TBIMOg2PM5INRv-Um11Lm8hf0lxxYaBf5BcfuAx4-7H-Qcp9OaQbsZrjBg7OXDloNG7cbOpzFiqBme_E7UkUi4H_EVY2Qma6J30xzcjl0oJj1BMVjqy_P4kIcGv-AyoetJt/?imgmax=800) ,
, ![clip_image104[1] clip_image104[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiIa5MoYkA1ws12O9wt20Ly1untiozetBV9EuKSE2TCFHP2BuPlc9LWwIAiTLl5byKO_S7D2EWMCyF9oUMVOuf7qEQ_RACQi3nDhB4B2d4c0k4Af3Nd-yVLYjKS0TIqh_LZvPgUK4sy1Qnn/?imgmax=800) , dan
, dan ![clip_image004[4] clip_image004[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi5b49BO-BOUyfM2FwmQiD4O1QAllDDNgMME7sk3b6FOP8JmiTooqWJ-s199ASn0s67vQqeli9dwIdlrHeCIzNnzb4XXkhjbAl6dHFyu6XtMU6mAn-CL997Z5dTgI6rjK612CHfi_kqto8F/?imgmax=800) adalah konstanta positif
adalah konstanta positif
 = keaktifan belajar
= keaktifan belajar
 = variabel pendorong
= variabel pendorong
Bentuk grafiknya secara umum adalah sebagai berikut.
Gambar 04 Grafik Fungsi Pengajaran
Fungsi pengajaran dalam ewkonomi dapat digunakan untuk menjelaskan fungsi biaya dan produksi.
Contoh:
Biaya produksi total (dalam jutaan rupiah) dari sebuah perusahaan dapat dinyatakan sebagai berikut.

![clip_image106[2] clip_image106[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhImVigwce_6iuPg_hBuyCV7r_zgrwErhaemc3CCaDz8v2-jjAzMygLdcn3pb6tf_C4CORJdgKdtw54Ew9baL-dq5FJ2UYR4x_WIU4qCJAX85bCHmaSw3n_lYyWOA3h8m-hhpzq05dBwieS/?imgmax=800) menyatakan biaya produksi dan
menyatakan biaya produksi dan  menyatakan kuantitas produksi
menyatakan kuantitas produksi
a. Berapa besar biaya tetapnya?
b. Bila berproduksi 100 unit, berapa besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya?
Penyelesaian:
Diketahui:![clip_image167[1] clip_image167[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg6W3a38BMabaEhvJ7pLNg408VUbUoouF7cLTph9y2qW4wAAV3eF8zFha26bOFTrxfsNu_uIOxUWe35PPTQnxxyqI0l4IvC7TsYyvGPcXUPvaE4STS2k3FgrPlc7Jt-GrO8-5GxyijlmpVq/?imgmax=800)
Ditanyakan:
a.![clip_image106[3] clip_image106[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEh587LajGKBxeO8_8bfuD0OhES3Nno5OQmyE_3auwefNH-XqdPQg-QJUa9Q6s83I1LfV-G8UgrkB9g1Sqfdhk1YB_WmG038DkamwGKwmz2FfbHmBpvgV1EW52fNYEWfdgNRzYt5tt6M1VAA/?imgmax=800) =......? jika
=......? jika 
b. Besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya =......? jika
Jawab:
a. Jika![clip_image173[1] clip_image173[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjwR75rDbaWKtqTvdTYwGKyNGLqogdvxB969XlVEbY7UW3uTR6T-_vdt2f192STD8LsCkQX_TPTM6G0Z4BVUWsgLBJ5b5i2Km4orC-gklc4rgpYrc9sNozRMHZaRbpl3SY75WU_SAy265VI/?imgmax=800) , maka
, maka ![clip_image106[4] clip_image106[4]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEiHB8u18q3CIv_c0y5PPLsHyGn1NFQPo6_zS7Ew5onZ0GOQrAD-XnEJgfLKgiosEo3fVDFI_kqOrZVU6-eo2nV6fDyOLGJdOAZhoZ9aHA8ZRbYPZ5b6tVw_azEVCcQN5tJHoWFyGsIqF3Ph/?imgmax=800) adalah
adalah
![clip_image167[2] clip_image167[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEir2RwZGLANUBprDYciteJXufY82YWpAOo_PP55U2nMUAdhhZJb6ojI0C-pdUhBNOryEzoqAC_8uW31Lm5bQd0KYlYNJg9mvDd01z8FAKr6v2f_TBORnydCGR5vNFaQg2M990KYwg6V6ryj/?imgmax=800)



Jadi biaya tetapnya adalah 50 juta rupiah
b. Jika![clip_image175[1] clip_image175[1]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgcaj0WNPxm1Oc_ZWjMpvrhLhSojPlxI0tucaX1ixCe9TukeQZJT__O9ve0I4aDkiAqAGmKowU3-6f9tZq13hgHBZFUOaDAnmgMR6vDJUUq3K0w1VF3yqT_HPpOQAYBbgeDC9VA3PxhHyYI/?imgmax=800) , maka
, maka ![clip_image106[5] clip_image106[5]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjcHnsB-VkEcEcEQHDvjNif6D4YNDpE9yDQeQBkGbI6pdbGaLPK-gBEto5EIp5ALWhudTzOXLO30_zPvdfV-RFdSixzsJ8mLoZjRjHu85fNtA7CwY_Os2js3j4q8mCBhiqVQX51pBiPyP2e/?imgmax=800) total adalah
total adalah
![clip_image167[3] clip_image167[3]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEi8GJszdlO0XsZatjPila9is9016vyLF-Q8Ri-NwqIBPKWNiEG01Iu5BUS-uz9VyT8fufn_VSvSt656vI94W0VPWibIb_4BdzLok49iA83ImsKay3_NR75wmkt_C-9XAcOy1ef6EuSms3A9/?imgmax=800)





Jadi, besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya (![clip_image175[2] clip_image175[2]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgdDpkeYgBkn39Rpb7z_QCE3Thj_NbIW_aWgpg7rihLlYNwWG2kwlrlzbo3RR5GPz4AiFWEAqCKHnqDuApkSLD6tTeqaaLnI7d7O2wnBccT_0VCwjxD_g37xKS2PmdVldgLub0tgEV0DJfz/?imgmax=800) ) adalah:
) adalah:


Dalam karya tulis ini fungsi pertumbuhan yang dimaksud hanya terbatas pada fungsi bunga majemuk, pertumbuhan penduduk atau biologis, kurva (fungsi) Gompertz, dan kurva (fungsi) pengajaran.
1. Fungsi Bunga Majemuk
Besarnya modal yang dibungakan tergantung dari waktu lamanya modal dibungakan asal tingkat bunga konstan. Jika modal (pokok) sebesar
Apabila
Dengan,
Jikan fungsi
Gambar 02 Grafik Fungsi Bunga Majemuk Dengan
Contoh:
Seorang petani membutuhkan uang sebesar 5 juta rupiah pada 10 tahun yang akan datang. Berapa jumlah uang yang harus ditabung mulai sekarang dengan bunga 24% per tahun untuk memperoleh jumlah uang yang diharapkan?
Penyelesaian:
Diketahui:
Ditanyakan:
Jawab:
Jadi, uang yang harus ditabung mulai sekarang sebesar Rp. 581772,49
2. Pertumbuhan Penduduk
Bila penduduk suatu negara (daerah) pada suatu saat
Bila suatu negara (daerah) dengan jumlah penduduk yang besar, maka pertumbuhan penduduk berlangsung hampir kontinyu, jumlah penduduk setelah t tahun menjadi:
Misalkan
Contoh:
Pada tahun 2001 penduduk sebuah kota adalah 629039 jiwa. Sedangkan pada tahun 2006 jumlah penduduknya adalah 771186 jiwa.
a. Berapa tingkat pertumbuhan penduduk kota tersebut?
b. Perkirakan jumlah penduduk kota tersebut pada tahun 2016!
Penyelesaian:
Diketahui:
t = 5 (dari 2001 sampai dengan 2006)
Ditanyakan:
a.
b.
Jawab:
a.
b. t = 15 (dari 2001 sampai dengan 2016)
Karena t cukup besar maka untuk mempermudah perhitungan kita gunakan logaritma, sehingga:
3. Fungsi Gompertz
Fungsi ini menggambarkan perkembangan yang lambat waktu mulai tumbuh, dan waktu mendekati asimtut batas pertumbuhan. Fungsi ini dinyatakan sebagai berikut.
Keterangan:
Sifat utama dari fungsi Gompertz digambarkan dengan dua jenis kurva di bawah ini.
Tipe I:
Tipe II:
Gambar 03 Kurva Gompertz
Kurva I, untuk nilai
Kurva yang ditemukan Gompertz ini dalam bidang ekonomi digunakan untuk fungsi pendapatan total dan produksi.
Contoh:
Penjualan setiap bulan dari sebuah perusahaan memenuhi fungsi
p adalah jumlah pengeluaran untuk promosi dan advertensi.
a. Berapa besar penjualan bila pengeluaran untuk promosi dan advertensi sama dengan nol atau berapa besar penjualan awalnya?
b. Berapa penjualan maksimumnya?
c. Berapa besar penjualannya bila pengeluaran untukpromosi dan avertensi 5?
Penyelesaian:
Diketahui:
Ditanyakan:
a.
b.
c.
Jawab:
a. Jika
Jadi penjualan awalnya adalah 100
b. Penjualan maksimum terjadi saat tingkat pertumbuhannya nol
Jadi, penjualan maksimunya adalah 1000
c. Jika
Jadi, besar penjualannya bila pengeluaran untuk promosi dan advertensi 5 adalah
4. Fungsi Pengajaran
Fungsi pengajaran umumnya dipakai oleh psikolog untuk menggambarkan taraf pertumbuhan pendidikan manusia, yang sifatnya meningkat cepat pada awalnya dan semakin lambat ketika mendekati asimtut batas pertumbuhan. Fungsi ini dinyatakan sebagai berikut.
Bentuk grafiknya secara umum adalah sebagai berikut.
Gambar 04 Grafik Fungsi Pengajaran
Fungsi pengajaran dalam ewkonomi dapat digunakan untuk menjelaskan fungsi biaya dan produksi.
Contoh:
Biaya produksi total (dalam jutaan rupiah) dari sebuah perusahaan dapat dinyatakan sebagai berikut.
a. Berapa besar biaya tetapnya?
b. Bila berproduksi 100 unit, berapa besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya?
Penyelesaian:
Diketahui:
Ditanyakan:
a.
b. Besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya =......? jika
Jawab:
a. Jika
Jadi biaya tetapnya adalah 50 juta rupiah
b. Jika
Jadi, besar proporsi biaya produksi tetapnya terhadap biaya produksi totalnya (



Wahh keren gan, lengkap banget artikel'a :D
ReplyDeleteKunjungi juga ya
Ikubaru Blogzia
bagus gan
ReplyDeletesayang sekli gak bisa di copy,padahal ada tugas buat cari fungsi eksponen dan logaritma
ReplyDelete