Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat
Berdasarkan rumus abc di atas, akar-akar persamaan kuadrat adalah sebagai berikut.

a. Jumlah akar-akar persamaan kuadrat
x1 + x2 =

Jadi, rumus jumlah akar-akar persamaan kuadrat adalah:

b. Hasil kali akar-akar persamaan kuadrat
x1 . x2 =
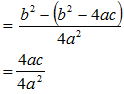
Jadi, rumus hasil kali akar-akar persamaan kuadrat adalah:

Bentuk-bentuk simetri akar-akar persamaan kuadrat
1) x12 + x22 = (x1 + x2)2 – 2x1x2 (jumlah kuadrat akar-akar)
2) x13 + x23 = (x1 + x2)3 – 3x1x2 (x1+x2)
Contoh:
1. Diketahui x1, x2 merupakan akar-akar dari persamaan kuadrat x2 – 3x + 5 = 0, tentukan nilai dari:
a. x1 + x2
b. x1 ・ x2
c. x12 + x22
d.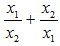
Jawab
1. x2 – 3x + 5 = 0
Dengan nilai a = 1, b = –3, c = 5, maka
a. x1 + x2 = –(-3)/1 = 3
b. x1 ・ x2 = 5/1 = 5
c. x12 + x22 = (x1 + x2)2 – 2x1x2
=( 3)2 – 2.5
= 9 – 10
= -1
d.
2. Jika jumlah kuadrat akar-akar persamaan x2 – 2x + k – 3 = 0 adalah 20 maka tentukan nilai k.
Jawab:
x2 – 2x + k – 3 = 0
Dengan nilai a = 1, b = –2, c = k – 3 maka
x1 + x2 = 2
x1 . x2 = k-3
Jumlah kuadrat akar-akarnya
x12 + x22 = 20
(x1 + x2)2 – 2x1x2 = 20
(2)2 -2(k-3) = 20
4 – 2(k-3) = 20
- 2(k-3) = 16
k-3 = -8
k = -5
Jadi nilai k = –5
Semoga bermanfaat :)

a. Jumlah akar-akar persamaan kuadrat
x1 + x2 =

Jadi, rumus jumlah akar-akar persamaan kuadrat adalah:

b. Hasil kali akar-akar persamaan kuadrat
x1 . x2 =
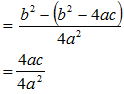
Jadi, rumus hasil kali akar-akar persamaan kuadrat adalah:
Bentuk-bentuk simetri akar-akar persamaan kuadrat
1) x12 + x22 = (x1 + x2)2 – 2x1x2 (jumlah kuadrat akar-akar)
2) x13 + x23 = (x1 + x2)3 – 3x1x2 (x1+x2)
Contoh:
1. Diketahui x1, x2 merupakan akar-akar dari persamaan kuadrat x2 – 3x + 5 = 0, tentukan nilai dari:
a. x1 + x2
b. x1 ・ x2
c. x12 + x22
d.
Jawab
1. x2 – 3x + 5 = 0
Dengan nilai a = 1, b = –3, c = 5, maka
a. x1 + x2 = –(-3)/1 = 3
b. x1 ・ x2 = 5/1 = 5
c. x12 + x22 = (x1 + x2)2 – 2x1x2
=( 3)2 – 2.5
= 9 – 10
= -1
d.

2. Jika jumlah kuadrat akar-akar persamaan x2 – 2x + k – 3 = 0 adalah 20 maka tentukan nilai k.
Jawab:
x2 – 2x + k – 3 = 0
Dengan nilai a = 1, b = –2, c = k – 3 maka
x1 + x2 = 2
x1 . x2 = k-3
Jumlah kuadrat akar-akarnya
x12 + x22 = 20
(x1 + x2)2 – 2x1x2 = 20
(2)2 -2(k-3) = 20
4 – 2(k-3) = 20
- 2(k-3) = 16
k-3 = -8
k = -5
Jadi nilai k = –5
Semoga bermanfaat :)
Post a Comment for "Jumlah dan Hasil Kali Akar-akar Persamaan Kuadrat"
Terima kasih atas komentar yang telah anda berikan