Rata-Rata Hitung, Rata-Rata Gabungan, Rata-Rata Ukur, dan Rata-Rata Harmonis
Rata-Rata Hitung (Mean)
1) Rata-Rata Hitung data tunggal
Rataan dari sekumpulan data yang banyaknya n adalah jumlah data dibagi dengan banyaknya data.
Keterangan:
n = banyaknya data
xi = data ke-i
Contoh
Tentukan nilai rata-rata hitung dari data 6, 4, 8, 10, 11, 10, 7
Jawab:
Jadi, rata-rata hitung dari data tersebut adalah 8
2) Rata-Rata Hitung data bergolong (berkelompok)
Rata-rata untuk data bergolong pada hakikatnya sama dengan menghitung rata-rata data pada distribusi frekuensi tunggal dengan mengambil titik tengah kelas sebagai xi.
Keterangan:
fi = frekuensi untuk nilai xi
xi = titik tengah kelas data ke-i
Contoh:
Tabel berikut menunjukkan data berat paket titipan barang pada suatu perusahaan
Berat Paket (gram)
|
Frekuensi
|
31-35
36-40
41-45
46-50
51-55
|
9
10
12
11
8
|
Jumlah
|
50
|
Rata-rata dari data tersebut adalah….(Soal UN SMK 2013)
Jawab:
Berat Paket (gram)
|
Frekuensi
|
xi
|
fi.xi
|
31-35
36-40
41-45
46-50
51-55
|
9
10
12
11
8
|
33
38
43
48
53
|
297
380
516
528
424
|
Jumlah
|
50
|
2145
|
Jadi, rata-rata dari data tersebut adalah 42,9 gram
Rata-Rata Gabungan
Jika terdapat beberapa kelompok data yang masing-masing rata-rata diketahui, kamu dapat menghitung rata-rata gabungan dari kelompok-kelompok data tersebut, seperti berikut. Misalnya,
...
maka rata-rata gabungannya dapat ditentukan dengan rumus:
Keterangan:
n1, n2, n3, …= jumlah data kelompok 1, kelompok 2, kelompok 3, dan seterusnya.
Contoh:
Nilai rata-rata ujian Bahasa Indonesia 39 siswa adalah 50. Jika seorang siswa yang dimasukkan dalam perhitungan rata-rata tersebut rata-ratanya menjadi 51, tentukan nilai ujian yang siswa tersebut.
Jawab:
Jadi nilai ujian siswa tersebut adalah 90
Rata-Rata Ukur (Rata-rata Geometris)
Jika perbandingan tiap dua data berurutan tetap atau hampir tetap, rata-rata ukur lebih baik digunakan dari pada rata-rata hitung, apabila dikehendaki rata-ratanya. Untuk data x1, x2, x3, x4, . . . , xn maka rata-rata ukur (U) didefinisikan sebagai berikut:
Contoh:
Hitunglah rata-rata ukur data berikut: 2, 4, 8, 4!
Jawab:
Jadi, rata-rata ukur data tersebut adalah 4
Rata-Rata Harmonis
Untuk data x1, x2, x3, x4, . . . ,xn, maka rata-rata harmonik (H) didefinisikan sebagai
berikut:
Contoh:
Hitunglah rata-rata harmonis dari data berikut: 3, 5, 6, 6, 7, 10, 12!
Jawab
Jadi, rata-rata harmonis dari data tersebut adalah 5,87
Semoga bermanfaat :)
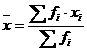

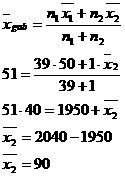


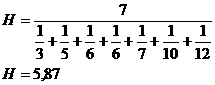
Terima kasih madematika
ReplyDeleteSangat membantu 👍
ReplyDeleteTerima kasih sudah membantu
ReplyDeleteYes
ReplyDelete