Menentukan Persamaan Garis Lurus
Ada beberapa kondisi yang perlu diperhatikan dalam menentukan persamaan garis lurus. Diantaranya kemiringan (gradien), titik yang dilalui garis tersebut serta kedudukannya dengan garis lain (sejajar atau saling tegak lurus). Berikut ini adalah beberapa cara yang dapat digunakan dalam menentukan persamaan garis lurus sesuai dengan ciri-ciri yang diketahui berhubungan dengan garis tersebut.
y - y1 = m(x – x1)
Contoh:
Tentukan persamaan garis yang melalui titik A(1, 3) dan bergradien 2
Jawab:
(1, 3) sehingga x1 = 1 dan y1 = 3
m = 2
y – y1 = m(x – x1)
y – 3 = 2(x – 1)
y – 3 = 2x – 2
y = 2x – 2 + 3
y = 2x + 1

Contoh:
Tentukan persamaan garis yang melalui titik A(3, –2) dan titik B(–1, 3)
Jawab:
A(3, –2) maka x1 = 3 dan y1 = -2
B(-1, 3) maka x2 = -1 dan y2 = 3
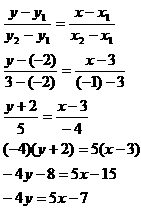
Syarat dua garis sejajar adalah
m1 = m2 atau m2 = m1
Dengan m1 adalah gradien garis yang sejajar dengan garis yang kita cari sedangkan m2 adalah gradien garis yang kita akan cari persamaanya. Sehingga, persamaan garis yang kita cari adalah persamaan garis lurus yang melalui titik (x1, y1) dan mempunyai kemiringan atau gradien (m2), yang dapat kita tentukan dengan formula
y - y1 = m2(x – x1)
Contoh:
Tentukan persamaan garis yang melalui titik A(–2, 3) dan sejajar garis y = –x – 5
Jawab:
y = -x – 5 maka m1 = -1
Karena garis sejajar maka m2 = m1 = -1
A(-2, 3) maka x1 = -2 dan y1 = 3
y - y1 = m2(x – x1)
y – 3 = -1(x – (-2))
y – 3 = -x – 2
y = -x + 1
m1 x m2 = -1 atau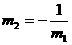
Dengan m1 adalah gradien garis yang sejajar dengan garis yang kita cari sedangkan m2 adalah gradien garis yang kita akan cari persamaanya. Sehingga, kita dapat menentukan persamaan garis tersebut dengan formula
y - y1 = m2(x – x1)
Contoh:
Tentukan persamaan garis yang melalui titik A(1, 4) dan tegak lurus dengan garis 2x – 5y = 6
Jawab:
2x – 5y = 6 maka m1 = 2/5
Karena garis tegak lurus maka

A(1, 4) maka x1 = 1 dan y1 = 4
y - y1 = m2(x – x1)
y – 4 = (5/2)(x – 1)
2(y – 4) = 5(x – 1)
2y – 4 = 5x – 5
2y = 5x -1
Semoga bermanfaat :)
A. Jika diketahui kemiringan (m) dan melalui satu titik (x1, y1)
Dalam menentukan persamaan garis lurus yang diketahui kemiringan atau gradiennya (m) serta satu titik (x1, y1) yang dilaluinya, kita dapat menggunakan formula berikut.y - y1 = m(x – x1)
Contoh:
Tentukan persamaan garis yang melalui titik A(1, 3) dan bergradien 2
Jawab:
(1, 3) sehingga x1 = 1 dan y1 = 3
m = 2
y – y1 = m(x – x1)
y – 3 = 2(x – 1)
y – 3 = 2x – 2
y = 2x – 2 + 3
y = 2x + 1
B. Jika diketahui melalui dua titik (x1, y1) dan (x2, y2)
Sebuah garis, dapat dilukis apabila minimal diketahui dua buah titik yang dilaluinya. Sama seperti halnya dengan melukis garis lurus pada bidang cartesius, suatu persamaan garis lurus dapat ditentukan apabila diketahui dua buah titik yang dilaluinya (x1, y1) dan (x2, y2). Dalam menentukan persamaan garis lurus yang melalui dua titik kita dapat menggunakan formula:
Contoh:
Tentukan persamaan garis yang melalui titik A(3, –2) dan titik B(–1, 3)
Jawab:
A(3, –2) maka x1 = 3 dan y1 = -2
B(-1, 3) maka x2 = -1 dan y2 = 3
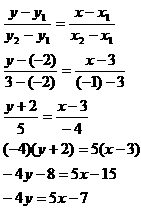
C. Jika diketahui melalui titik (x1, y1) dan sejajar dengan garis lain
Ciri dua buah garis atau lebih yang saling sejajar adalah mempunyai nilai kemiringan atau gradien yang sama. Dalam kasus dimana diketahui melalui satu titik (x1, y1) dan sejajar garis lain, kita dapat menentukan persamaan garisnya dengan menentukan gradien garis yang diketahui terlebihdahulu, kemudian kita dapat menentukan gradient garis yang sedang kita cari dimanaSyarat dua garis sejajar adalah
m1 = m2 atau m2 = m1
Dengan m1 adalah gradien garis yang sejajar dengan garis yang kita cari sedangkan m2 adalah gradien garis yang kita akan cari persamaanya. Sehingga, persamaan garis yang kita cari adalah persamaan garis lurus yang melalui titik (x1, y1) dan mempunyai kemiringan atau gradien (m2), yang dapat kita tentukan dengan formula
y - y1 = m2(x – x1)
Contoh:
Tentukan persamaan garis yang melalui titik A(–2, 3) dan sejajar garis y = –x – 5
Jawab:
y = -x – 5 maka m1 = -1
Karena garis sejajar maka m2 = m1 = -1
A(-2, 3) maka x1 = -2 dan y1 = 3
y - y1 = m2(x – x1)
y – 3 = -1(x – (-2))
y – 3 = -x – 2
y = -x + 1
D. Jika diketahui melalui titik (x1, y1) dan tegak lurus dengan garis lain
Sedangkan, apabila persamaan garis yang kita akan cari melalui suatu titik (x1, y1) dan tegak lurus dengan garis lain kita harus memahami bahwa syarat dua garis atau lebih saling tegak lurus adalah hasil perkalian gradienya adalah -1m1 x m2 = -1 atau
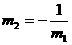
Dengan m1 adalah gradien garis yang sejajar dengan garis yang kita cari sedangkan m2 adalah gradien garis yang kita akan cari persamaanya. Sehingga, kita dapat menentukan persamaan garis tersebut dengan formula
y - y1 = m2(x – x1)
Contoh:
Tentukan persamaan garis yang melalui titik A(1, 4) dan tegak lurus dengan garis 2x – 5y = 6
Jawab:
2x – 5y = 6 maka m1 = 2/5
Karena garis tegak lurus maka

A(1, 4) maka x1 = 1 dan y1 = 4
y - y1 = m2(x – x1)
y – 4 = (5/2)(x – 1)
2(y – 4) = 5(x – 1)
2y – 4 = 5x – 5
2y = 5x -1
Semoga bermanfaat :)
Lengkap *w*)/ Thx ya~
ReplyDeleteKeren gan (y)
ReplyDeletepaling nyebelin dari bikin artikel matematika di blog adalah rumusnya..hehehhe..gak bisa ditulis langsung harus pake gambar..heehhe..
ReplyDeletesalam kenal bro..dari PorosIlmu.com
kalo soal
ReplyDelete3y+6=4x+10
Kalau nentuin persamaan garis lurus yang sejajar dengan 2x+3y-6=0 tanpa diketahui titik atau yang lain itu gimana ya?
ReplyDelete2x+3y-6=0
Delete3y=-2x+6
y=2x+6 dibagi 3
y=2/3x+2