Cara Mencari Akar Tanpa Menggunakan Kalkulator
Kemudahan yang disediakan gadget saat ini, membuat kita lupa pentingnya suatu proses. Hasil yang instan membuat indera kita kian manja. Akibatnya, ketajaman dalam berpikir manusia saat ini cenderung berkurang dan sangat bergantung pada gadget.
Kalkulator merupakan salah satu temuan modern yang membantu manusia untuk melakukan operasi hitung seperti penjumlahan, pengurangan, perkalian, dan pembagian dengan mudah. Dengan menggunakan kalkulator manusia tidak harus repot-repot beripikir tinggal menekan tombol yang ada pada kalkulator dan munculah hasilnya secara instan. Bahkan, tidak hanya itu kalkulator zaman modern sudah dilengkapi dengan berbagai fitur operasi tambahan seperti logaritma, trigonometri, faktorial, kombinasi, permutasi, akar, pangkat dan masih banyak lagi.
Karena ketergantungan pada kalkulator kita lupa bagaimana prosesnya. Dalam artikel kali ini, akan dibahas mengnai mencari akar tanpa menggunakan kalkulator. Mencari akar suatu bilangan sangat dimungkinkan secara manual atau tanpa menggunakan kalkulator, tiga cara praktis yang dapat digunakan adalah membagi bilangan yang diakarkan dengan faktor primanya (menjabarkan kedalam bentuk pohon faktor), menebak/menaksirnya, dan menggunakan cara bersusun untuk menentukan akar suatu bilangan. Sebagai tambahan pula dalam artikel ini akan dibahas mengenai penyederhanaan bentuk akar.
Berikut ini adalah contoh soal penyederhanaan bentuk akar
Contoh 1
Sederhanakan bentuk $\sqrt{48}$!
Penyelesaian
Caranya adalah ubah 48 menjadi perkalian dua bilangan dengan ketentuan salah satu bilangan dapat diakarkan. Bilangan yang dapat diakarkan adalah bilangan terbesar. 48 dapat diubah menjadi 4 x 12 dan 16 x 3, maka yang kita pilih adalah 16 x 3 agar nantinya kita mendapat bentuk akar yang paling sederhana/terkecil
$\sqrt{48} = \sqrt{16 \times 3} = 4\sqrt{3}$
Contoh 2
Sederhanakan bentuk $\sqrt{338}$!
Penyelesaian
$\sqrt{338} = \sqrt{169 \times 2} = 13\sqrt{2}$
Bagaimana agar lebih mudah menyederhanakannya? Kuncinya adalah coba bagi bilangan yang akan disederhanakan mulai dari bilangan positif 2, 3, 5, 6, dan seterusnya. Kecuali 1 dan bilangan kuadrat sempurna yaitu 4, 9, 16, 25, dan seterusnya. Mulailah mencoba membaginya dengan bilangan yang terkecil hingga didapatkan faktor lain yang berupa bilangan kuadrat sempurna.
Menentukan nilai akar suatu bilangan dengan menjabarkannya ke dalam bentuk perkalian bilangan primanya mungkin adalah salah satu cara yang paling mudah. Cara seperti ini dapat juga dilakukan dengan menjabarkan suatu bilangan ke dalam pohon faktor. Namun, cara ini hanya berhasil apabila akar yang dicari merupakan bilangan kuadrat sempurna. Jika tidak, maka cara ini tidak akan berhasil dan tentunya kita harus mencari cara lain untuk menentukan akar. Untuk lebih jelasnya perhatikan contoh berikut
Contoh 3
Tentukan nilai dari $\sqrt{1156}$!!
Penyelesaian
1156 = 2 x 2 x 17 x 17, sehingga diperoleh
$\sqrt{1156} = \sqrt{2 \times 2 \times 17 \times 17}$$ =\sqrt{2^2 \times 17^2} = 2 \times 17 = 34$
Contoh 4
Tentukan nilai dari $\sqrt{1764}$
Penyelesaian
1764 = 2 x 2 x 3 x 3 x 7 x 7
$\sqrt{1764}= \sqrt{2 \times 2 \times 3 \times 3 \times 7 \times 7}$$ = \sqrt{2^2 \times 3^2 \times 7^2} = 2 \times 3 \times 7 = 42$
$1^2 = 1$
$2^2 = 4$
$3^2 = 9$
$4^2 = 16$
$5^2 = 25$
$6^2 = 36$
$7^2 = 49$
$8^2 = 64$
$9^2 = 81$
$10^2 = 100$
$20^2 = 400$
$30^2 = 900$
dan seterusnya
Jika dilihat pada pengkuadratan 1 hingga 9, maka akan menghasilkan angka satuan secara berturut-turut
$1^2 = 1$
$2^2 = 4$
$3^2 = 9$
$4^2 = ..6$
$5^2 = ..5$
$6^2 = ..6$
$7^2 = ..9$
$8^2 = ..4$
$9^2 = ..1$
Ini yang akan digunakan sebagai dasar menaksir/menebak akar kuadrat yang sedang dicari. Untuk lebih jelasnya perhatikan contoh soal berikut
Contoh 5
Nilai dari $\sqrt{6889}$ adalah ...
Penyelesaian
$\sqrt{6889}$, hasil akar dari bilangan tersebut adalah lebih dari 80, karena $80^2 = 6400$ akibatnya hasil akarnya terdiri dari 2 angka dengan angka pertama 8. Angka kedua dapat kita taksir dengan melihat angka satuan dari akar yang dicari yaitu 9. Angka 9 kemungkinan dihasilkan oleh pengkuadratan 3 dan 7, setelah dicoba-coba hasil yang paling tepat adalah 87. Jadi, nilai dari $\sqrt{6889}$ adalah 87
Contoh 6
Tentukan nilai dari $\sqrt{15376}$
Penyelesaian
$\sqrt{15376}$, hasil akar dari bilangan tersebut adalah lebih dari 100, karena $100^2 = 10000$
akibatnya akan ada 3 angka hasil akar $\sqrt{15376}$ dengan angka pertama 1. Angka kedua kita taksir dengan mencoba-coba diperoleh yang paling medekati adalah 120 (sebab $120^2 = 14400$) dengan demikian angka yang kedua adalah 2. Tinggal angka yang ketiga yang perlu ditaksir, lihatlah jika $\sqrt{15376}$, angka terakhirnya adalah 6, angka satuan yang dikuadratkan menghasilkan angka satuan 6 adalah 4 dan 6, setelah dicoba mengkuadratkan angka 124 dan 126 diperoleh lah $\sqrt{15376} = 124$. Jadi, akar dari $\sqrt{15376}$ adalah 124.
Cara yang terakhir ini dikenal juga dengan "Longhand Method", saya belum menemukan bahasa Indonesia yang tepat untuk metode ini. Prinsip dari menentukan nilai akar dengan cara bersusun atau "Longhand Method" ini hampir sama seperti pembagian bersusun. Namun jika dibandingkan dengan menggunakan kalkulator, metode ini memang agak ribet. Keunggulan dari metode ini adalah penggunaan yang tidak terbatas dari bilangan kuadrat sempurna saja. Dengan demikian kita dapat menentukan akar suatu bilangan tanpa khawatir apakah itu bilangan kuadrat sempurna atau tidak dan bahkan bilangan pecahan desimal dapat kita cari akarnya dengan menggunakan metode ini.
Langkah-langkah dalam menentukan akar dngan cara bersusun adalah
Untuk lebih jelasnya perhatikan contoh berikut
Contoh 7
Nilai dari $\sqrt{1,6129}$ adalah ...
Penyelesaian
Menuliskan bentuk akar yang dicari, jangan lupa tuliskan juga akar pangkatnya yang dalam hal ini adalah angka 2. Kelompokkan angka-angka yang diakarkan dalam hal ini kita kelompokan menjadi terdiri dari dua bilangan dan kelompokkan mulai dari belakang. Dalam hal ini 1,6129 maka menjadi 1,|61|29
Kemudian cari bilangan yang jika dikuadratkan hasilnya mendekati (kurang atau sama dengan) bilangan kelompok pertama/paling depan. Jika sudah ditemukan, tulis di atas akar dan hasil kuadratnya tulis di bawah bilangan kelompok pertama. Kurangkan bilangan kelompok pertama dengan hasil kuadrat bilangan tadi. Bilangan yang paling tepat adalah 1
Langkah berikutnya, kita akan mencari bilangan yang mendekati (kurang atau sama dengan) bilangan sisa pengurangan sebelumnya. Caranya adalah dengan mengalikan 2 bilangan di atas tanda akar kemudian tambahkan sebuah angka/bilangan dibelakangnya dengan ketentuan apabila dikali angka itu sendiri hasilnya adalah bilangan yang paling mendekati sisa bilangan sebelumnya. 1 dikali 2 adalah 2, angka yang paling tepat ditempatkan dibelakang 2 adalah 2 karena 22 x 2 = 44 adalah angka yang paling mendekati 61. Tuliskan pula tanda koma (,) di depan 2.
Pengulangan langkah sebelumnya, 12 dikali 2 adalah 24. Angka yang paling tepat ditambahkan dibelakang 24 adalah 7 karena 247 x 7 adalah 1729, sehingga sisanya sama dengan 0.
Jadi, nilai dari $\sqrt{1,6129}$ adalah 1,27
Contoh 8
Tentukan nilai $\sqrt{3}$!
Penyelesaian
Angka 3 apabila dikelompokan maka dapat ditulis 3,|00|00|00|00 ....dst. Kali ini saya hanya akan tulis 3 saja.
Bilangan yang paling tepat jika dikuadratkan hasilnya mendekati 3 adalah 1. Sisa dari penguranganya adalah 2 dan ingat turunkan pula kelompok yang kedua yaitu 00 sehingga sisanya ditulis 200
1 dikali 2 adalah 2, bilangan dibelakang 2 yang paling tepat agar hasil kali dengan bilangan itu sendiri mendekati 200 adalah 7. Karena 27 x 7 = 189
17 dikali 2 adalah 34, bilangan dibelakang 34 yang paling tepat agar hasil kali dengan bilangan itu sendiri mendekati 1100 adalah 3. Karena 343 x 3 = 1029
173 dikali 2 adalah 346, bilangan dibelakang 346 yang paling tepat agar hasil kali dengan bilangan itu sendiri mendekati 7100 adalah 2. Karena 3462 x 2 = 6924. Perhitungan saya cukupkan sampai di sini mengginat $\sqrt{3}$ adalah bilangan irrasional
Jadi, nilai dari $\sqrt{3} = 1,732...$
Agar lebih yakin anda bisa membuktikan metode di atas dengan menggunakan kalkulator. Nah, demikianlah mengenai cara mencari akar dalam hal ini adalah akar kuadrat tanpa menggunakan kalkulator. Artikel lainnya juga akan membahas mengenai cara menentukan akar pangkat 3 tanpa menggunakan kalkulator. Semoga dapat dipahami dan bermanfaat.
Karena ketergantungan pada kalkulator kita lupa bagaimana prosesnya. Dalam artikel kali ini, akan dibahas mengnai mencari akar tanpa menggunakan kalkulator. Mencari akar suatu bilangan sangat dimungkinkan secara manual atau tanpa menggunakan kalkulator, tiga cara praktis yang dapat digunakan adalah membagi bilangan yang diakarkan dengan faktor primanya (menjabarkan kedalam bentuk pohon faktor), menebak/menaksirnya, dan menggunakan cara bersusun untuk menentukan akar suatu bilangan. Sebagai tambahan pula dalam artikel ini akan dibahas mengenai penyederhanaan bentuk akar.
Menyederhanakan Bentuk Akar
Bagian pertama pada artikel ini akan membahas mengenai menyederhanakan bentuk akar. Menyederhanakan bentuk akar dalam hal ini kita mencari hasil akarnya namun belum dikatakan selesai. Karena dalam penyedehanaan ini, nantinya masih akan berupa bentuk akar namun lebih sederhana. Keterampilan dalam memecah suatu bilangan sangat diperlukan disini.Berikut ini adalah contoh soal penyederhanaan bentuk akar
Contoh 1
Sederhanakan bentuk $\sqrt{48}$!
Penyelesaian
Caranya adalah ubah 48 menjadi perkalian dua bilangan dengan ketentuan salah satu bilangan dapat diakarkan. Bilangan yang dapat diakarkan adalah bilangan terbesar. 48 dapat diubah menjadi 4 x 12 dan 16 x 3, maka yang kita pilih adalah 16 x 3 agar nantinya kita mendapat bentuk akar yang paling sederhana/terkecil
$\sqrt{48} = \sqrt{16 \times 3} = 4\sqrt{3}$
Contoh 2
Sederhanakan bentuk $\sqrt{338}$!
Penyelesaian
$\sqrt{338} = \sqrt{169 \times 2} = 13\sqrt{2}$
Bagaimana agar lebih mudah menyederhanakannya? Kuncinya adalah coba bagi bilangan yang akan disederhanakan mulai dari bilangan positif 2, 3, 5, 6, dan seterusnya. Kecuali 1 dan bilangan kuadrat sempurna yaitu 4, 9, 16, 25, dan seterusnya. Mulailah mencoba membaginya dengan bilangan yang terkecil hingga didapatkan faktor lain yang berupa bilangan kuadrat sempurna.
Menentukan Nilai Akar Dengan Mejabarkan ke dalam Bentuk Perkalian Bilangan Prima
Menentukan nilai akar suatu bilangan dengan menjabarkannya ke dalam bentuk perkalian bilangan primanya mungkin adalah salah satu cara yang paling mudah. Cara seperti ini dapat juga dilakukan dengan menjabarkan suatu bilangan ke dalam pohon faktor. Namun, cara ini hanya berhasil apabila akar yang dicari merupakan bilangan kuadrat sempurna. Jika tidak, maka cara ini tidak akan berhasil dan tentunya kita harus mencari cara lain untuk menentukan akar. Untuk lebih jelasnya perhatikan contoh berikutContoh 3
Tentukan nilai dari $\sqrt{1156}$!!
Penyelesaian
1156 = 2 x 2 x 17 x 17, sehingga diperoleh
$\sqrt{1156} = \sqrt{2 \times 2 \times 17 \times 17}$$ =\sqrt{2^2 \times 17^2} = 2 \times 17 = 34$
Contoh 4
Tentukan nilai dari $\sqrt{1764}$
Penyelesaian
1764 = 2 x 2 x 3 x 3 x 7 x 7
$\sqrt{1764}= \sqrt{2 \times 2 \times 3 \times 3 \times 7 \times 7}$$ = \sqrt{2^2 \times 3^2 \times 7^2} = 2 \times 3 \times 7 = 42$
Menetukan Nilai Akar Dengan Cara Menaksir/Menebaknya
Menebak bukan berarti menebak secara sembarangan, dan cara ini juga hanya bisa dilakukan apabila akar yang di cari adalah berupa akar bilangan kuadrat sempurna. Hal yang harus dipahami sebelum menebak adalah dengan memahami bentuk pangkat dua berikut$1^2 = 1$
$2^2 = 4$
$3^2 = 9$
$4^2 = 16$
$5^2 = 25$
$6^2 = 36$
$7^2 = 49$
$8^2 = 64$
$9^2 = 81$
$10^2 = 100$
$20^2 = 400$
$30^2 = 900$
dan seterusnya
Jika dilihat pada pengkuadratan 1 hingga 9, maka akan menghasilkan angka satuan secara berturut-turut
$1^2 = 1$
$2^2 = 4$
$3^2 = 9$
$4^2 = ..6$
$5^2 = ..5$
$6^2 = ..6$
$7^2 = ..9$
$8^2 = ..4$
$9^2 = ..1$
Ini yang akan digunakan sebagai dasar menaksir/menebak akar kuadrat yang sedang dicari. Untuk lebih jelasnya perhatikan contoh soal berikut
Contoh 5
Nilai dari $\sqrt{6889}$ adalah ...
Penyelesaian
$\sqrt{6889}$, hasil akar dari bilangan tersebut adalah lebih dari 80, karena $80^2 = 6400$ akibatnya hasil akarnya terdiri dari 2 angka dengan angka pertama 8. Angka kedua dapat kita taksir dengan melihat angka satuan dari akar yang dicari yaitu 9. Angka 9 kemungkinan dihasilkan oleh pengkuadratan 3 dan 7, setelah dicoba-coba hasil yang paling tepat adalah 87. Jadi, nilai dari $\sqrt{6889}$ adalah 87
Contoh 6
Tentukan nilai dari $\sqrt{15376}$
Penyelesaian
$\sqrt{15376}$, hasil akar dari bilangan tersebut adalah lebih dari 100, karena $100^2 = 10000$
akibatnya akan ada 3 angka hasil akar $\sqrt{15376}$ dengan angka pertama 1. Angka kedua kita taksir dengan mencoba-coba diperoleh yang paling medekati adalah 120 (sebab $120^2 = 14400$) dengan demikian angka yang kedua adalah 2. Tinggal angka yang ketiga yang perlu ditaksir, lihatlah jika $\sqrt{15376}$, angka terakhirnya adalah 6, angka satuan yang dikuadratkan menghasilkan angka satuan 6 adalah 4 dan 6, setelah dicoba mengkuadratkan angka 124 dan 126 diperoleh lah $\sqrt{15376} = 124$. Jadi, akar dari $\sqrt{15376}$ adalah 124.
Menentukan Nilai Akar Dengan Cara Bersusun
Cara yang terakhir ini dikenal juga dengan "Longhand Method", saya belum menemukan bahasa Indonesia yang tepat untuk metode ini. Prinsip dari menentukan nilai akar dengan cara bersusun atau "Longhand Method" ini hampir sama seperti pembagian bersusun. Namun jika dibandingkan dengan menggunakan kalkulator, metode ini memang agak ribet. Keunggulan dari metode ini adalah penggunaan yang tidak terbatas dari bilangan kuadrat sempurna saja. Dengan demikian kita dapat menentukan akar suatu bilangan tanpa khawatir apakah itu bilangan kuadrat sempurna atau tidak dan bahkan bilangan pecahan desimal dapat kita cari akarnya dengan menggunakan metode ini.Langkah-langkah dalam menentukan akar dngan cara bersusun adalah
- Menuliskan bentuk akar yang dicari, jangan lupa tuliskan juga akar pangkatnya yang dalam hal ini adalah angka 2. Kelompokkan angka-angka yang diakarkan dalam hal ini kita kelompokan menjadi terdiri dari dua bilangan dan kelompokkan mulai dari belakang. Contoh: 123456 maka dikelompokan menjadi 12|34|56. Seandainya bilangannya desimal maka kelompokan mulai dari tanda koma baik ke depan tanda koma maupun ke belakang tanda koma. Contoh: 123,456 maka dikelompokkan menjadi 1|23,|45|60. Bisa juga kita batasi dengan spasi sehingga dapat ditulis 1 23, 45 60
- Kemudian cari bilangan yang jika dikuadratkan hasilnya mendekati (kurang atau sama dengan) bilangan kelompok pertama/paling depan. Jika sudah ditemukan, tulis di atas akar dan hasil kuadratnya tulis di bawah bilangan kelompok pertama. Kurangkan bilangan kelompok pertama dengan hasil kuadrat bilangan tadi.
- Langkah berikutnya, kita akan mencari bilangan yang mendekati (kurang atau sama dengan) bilangan sisa pengurangan sebelumnya. Caranya adalah dengan mengalikan 2 bilangan di atas tanda akar kemudian tambahkan sebuah angka/bilangan dibelakangnya dengan ketentuan apabila dikali angka itu sendiri hasilnya adalah bilangan yang paling mendekati sisa bilangan sebelumnya. Langkah dapat diulang terus sampai sisa bilangannya sama dengan 0.
Untuk lebih jelasnya perhatikan contoh berikut
Contoh 7
Nilai dari $\sqrt{1,6129}$ adalah ...
Penyelesaian
Menuliskan bentuk akar yang dicari, jangan lupa tuliskan juga akar pangkatnya yang dalam hal ini adalah angka 2. Kelompokkan angka-angka yang diakarkan dalam hal ini kita kelompokan menjadi terdiri dari dua bilangan dan kelompokkan mulai dari belakang. Dalam hal ini 1,6129 maka menjadi 1,|61|29
Contoh 8
Tentukan nilai $\sqrt{3}$!
Penyelesaian
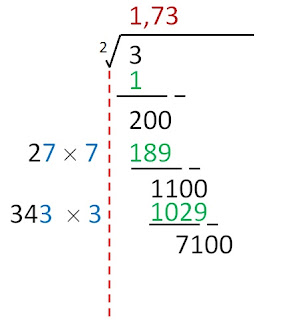
Angka 3 apabila dikelompokan maka dapat ditulis 3,|00|00|00|00 ....dst. Kali ini saya hanya akan tulis 3 saja.
Agar lebih yakin anda bisa membuktikan metode di atas dengan menggunakan kalkulator. Nah, demikianlah mengenai cara mencari akar dalam hal ini adalah akar kuadrat tanpa menggunakan kalkulator. Artikel lainnya juga akan membahas mengenai cara menentukan akar pangkat 3 tanpa menggunakan kalkulator. Semoga dapat dipahami dan bermanfaat.
Ah serius ga nie pak Caranya
ReplyDelete