Mengenal Fungsi atau Pemetaan dan Contoh Soalnya
Relasi dari dua himpunan misalkan himpunan A dan himpunan B merupakan hubungan yang memasangkan anggota A dan anggota B. Dalam relasi dikenal pula istilah pemetaan atau fungsi. Fungsi dalam hal ini bukan kegunaan suatu benda melainkan fungsi masih ada kaitannya antara hubungan antara dua himpunan
Contoh 1
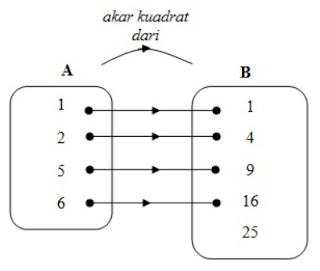
Diketahui himpunan A = {1, 2, 3, 4} dan himpunan B ={1, 4, 9, 16, 25}. Jika relasi dari himpunan A ke B merupakan relasi "akar kuadrat dari". Nyatakan relasi tersebut dengan diagram panah dan apakah relasi tersebut dapat dikatakan sebagai fungsi?
Jawab
A = {1, 2, 3, 4}
B ={1, 4, 9, 16, 25}
Relasi himpunan A ke himpunan B merupakan fungsi karena setiap anggota A memiliki pasangan tepat satu dengan anggota himpunan B
Pada dasarnya setiap fungsi merupakan sebuah relasi, namun untuk setiap relasi belum tentu merupakan sebuah fungsi. Untuk membedakan relasi yang merupakan fungsi dan bukan fungsi sebenarnya sangat mudah. Kita lihat saja anggota yang menjadi daerah asal, jika setiap anggota yang menjadi daerah asal telah memiliki pasangan dan tepat satu dengan anggota daerah kawannya maka dapat dikatakan relasi tersebut fungsi dan jika tidak maka bukan fungsi.
Dalam beberapa kasus tertentu kita sering dihadapkan pada masalah fungsi dan bukan fungsi. Misalkan kita dihadapkan pada soal-soal yang biasanya relasi tersbut dapat dinyatakan dengan diagram panah, himpunan pasangan berurutan, maupun grafik cartesius. Untuk membedakan relasi yang merupakan fungsi dan bukan fungsi pada diagram panah tinggal dilihat daerah asalnya yang biasanya dibuat pada kurva yang di sebelah kiri, pastikan setiap anggotanya telah memiliki pasangan dan tepat hanya satu saja.Pada himpunan pasangan berurutan, biasanya anggota daerah asal ditulis di sebelah kiri pada setiap pasangan. Jadi, jika anggota daerah asal tersebut ditulis lbih dari satu kali maka sudah dapat dipastikan itu bukan fungsi. Sedangkan pada grafik cartesius, kita harus pahami jika anggota pada sumbu x merupakan daerah asal dan kita tinggal lihat apakah setiap anggota daerah asal telah memiliki satu pasangan saja atau tidak dengan kata lain tidak ada lebih dari satu titik yang segaris secara vertikal. Biasanya grafik-grafik berupa lingkaran sudah dapat dikatakan bukan merupakan sebah fungsi
Contoh 2
Manakah diantara himpunan pasangan berurutan berikut yang merupakan sebuah fungsi
(i) {(2, 1), (3, 1), (4, 1), (5, 2)}
(ii) {(1, 2), (1, 3), (2, 1), (2, 3)}
(iii) {(3, 5), (4, 6), (6, 7), (8, 9)}
(iv) {(2, 2), (2, 4), (2, 6), (2, 8)}
Jawab
(i) {(2, 1), (3, 1), (4, 1), (5, 2)} merupakan fungsi
(ii) {(1, 2), (1, 3), (2, 1), (2, 3)} merupakan relasi/bukan fungsi
(iii) {(3, 5), (4, 6), (6, 7), (8, 9)} merupakan fungsi
(iv) {(2, 2), (2, 4), (2, 6), (2, 8)} merupakan relasi/bukan fungsi
Jadi, impunan pasangan berurutan berikut yang merupakan sebuah fungsi ditunjukkan oleh nomor (i) dan (iii)
Diagram panah di atas merupakan sebuah fungsi. Yang dapat dikatakan domain atau daerah asal adalah semua anggota himpunan A ={1, 2, 3, 4}. Kodomain atau daerah lawan/kawan adalah anggota semua anggota himpunan B = {1, 4, 9, 16, 25}. Sedangkan range adalah anggota kodomain yang memiliki pasangan dengan anggota domain dalam hal ini adalah {1, 4, 9, 16}
Contoh 3
Diketahui fungsi f dinotasikan dengan f : x $\rightarrow$ 2x + 3. Jika diketahui domain dari fungsi f adalah {0, 1, 2, 3} dan kodomainya adalah bilangan bulat. Tentukan
a. Rumus fungsi f
b. Daerah hasil f
c. Tentukan nilai x jika f(x) = 17
d. Tentukan nilai a jika f(a) = -1
Jawab
a. f(x) = 2x + 3
b. f(x) = 2x + 3
f(0) = 2(0) + 3 = 3
f(1) = 2(1) + 3 = 5
f(2) = 2(2) + 3 = 7
f(3) = 2(3) + 3 = 9
Daerah hasil = {3, 5, 7, 9}
c. f(x) = 17
2x + 3 = 17
2x = 17 - 3
2x = 14
x = 7
d. f(a) = -1
2a + 3 = -1
2a = -1 - 2
2a = -4
a = -2
Contoh 4
Jika diketahui fungsi g(x) = ax + b dengan g(2) = 4 dan g(-3) = -11, tentukan
a. Nilai a dan b
b. Rumus fungsi g
c. Peta dari 3
Jawab
a. g(x) = ax + b
g(2) = 4 maka 2a + b = 4
g(-3) = -11 maka -3a + b = -11
Eliminasi b
2a + b = 4
-3a + b = -11 -
5a = 15
a = 3
Substitusi a = 3 ke 2a + b = 4
2(3) + b = 4
6 + b = 4
b = 4 - 6
b = -2
Jadi, nilai a = 3 dan b = -2
b. g(x) = 3x - 2
c. g(x) = 3x -2
g(3) = 3(3) - 2 = 7
Jadi, peta dari 3 adalah 7
Pengertian Fungsi
Fungsi dalam matematika dikenal pula dengan sebutan pemetaan. Fungsi atau pemetaan dari suatu himpunan misalkan himpunan A ke himpunan B merupakan relasi khusus yang memasangkan setiap anggota himpunan A tepat satu pasangan dengan anggota himpunan B. Disini ditekankan kata setiap dan tepat satu pasangan, ini berarti setiap anggota himpunan A tanpa terkecuali harus memiliki hanya satu pasanga dengan anggota himpunan B. Sedangkan untuk anggota himpunan B tidak berlaku aturan tersebut, dengan kata lain mungkin saja anggota B memiliki pasangan lebih dari satu pasangan dengan anggota himpunan A atau terdapat anggota himpunan B yang tidak memiliki pasangan.Contoh 1
Diketahui himpunan A = {1, 2, 3, 4} dan himpunan B ={1, 4, 9, 16, 25}. Jika relasi dari himpunan A ke B merupakan relasi "akar kuadrat dari". Nyatakan relasi tersebut dengan diagram panah dan apakah relasi tersebut dapat dikatakan sebagai fungsi?
Jawab
A = {1, 2, 3, 4}
B ={1, 4, 9, 16, 25}
Relasi himpunan A ke himpunan B merupakan fungsi karena setiap anggota A memiliki pasangan tepat satu dengan anggota himpunan B
Pada dasarnya setiap fungsi merupakan sebuah relasi, namun untuk setiap relasi belum tentu merupakan sebuah fungsi. Untuk membedakan relasi yang merupakan fungsi dan bukan fungsi sebenarnya sangat mudah. Kita lihat saja anggota yang menjadi daerah asal, jika setiap anggota yang menjadi daerah asal telah memiliki pasangan dan tepat satu dengan anggota daerah kawannya maka dapat dikatakan relasi tersebut fungsi dan jika tidak maka bukan fungsi.
Dalam beberapa kasus tertentu kita sering dihadapkan pada masalah fungsi dan bukan fungsi. Misalkan kita dihadapkan pada soal-soal yang biasanya relasi tersbut dapat dinyatakan dengan diagram panah, himpunan pasangan berurutan, maupun grafik cartesius. Untuk membedakan relasi yang merupakan fungsi dan bukan fungsi pada diagram panah tinggal dilihat daerah asalnya yang biasanya dibuat pada kurva yang di sebelah kiri, pastikan setiap anggotanya telah memiliki pasangan dan tepat hanya satu saja.Pada himpunan pasangan berurutan, biasanya anggota daerah asal ditulis di sebelah kiri pada setiap pasangan. Jadi, jika anggota daerah asal tersebut ditulis lbih dari satu kali maka sudah dapat dipastikan itu bukan fungsi. Sedangkan pada grafik cartesius, kita harus pahami jika anggota pada sumbu x merupakan daerah asal dan kita tinggal lihat apakah setiap anggota daerah asal telah memiliki satu pasangan saja atau tidak dengan kata lain tidak ada lebih dari satu titik yang segaris secara vertikal. Biasanya grafik-grafik berupa lingkaran sudah dapat dikatakan bukan merupakan sebah fungsi
Contoh 2
Manakah diantara himpunan pasangan berurutan berikut yang merupakan sebuah fungsi
(i) {(2, 1), (3, 1), (4, 1), (5, 2)}
(ii) {(1, 2), (1, 3), (2, 1), (2, 3)}
(iii) {(3, 5), (4, 6), (6, 7), (8, 9)}
(iv) {(2, 2), (2, 4), (2, 6), (2, 8)}
Jawab
(i) {(2, 1), (3, 1), (4, 1), (5, 2)} merupakan fungsi
(ii) {(1, 2), (1, 3), (2, 1), (2, 3)} merupakan relasi/bukan fungsi
(iii) {(3, 5), (4, 6), (6, 7), (8, 9)} merupakan fungsi
(iv) {(2, 2), (2, 4), (2, 6), (2, 8)} merupakan relasi/bukan fungsi
Jadi, impunan pasangan berurutan berikut yang merupakan sebuah fungsi ditunjukkan oleh nomor (i) dan (iii)
Notasi dan Istilah dalam Fungsi
Fungsi atau pemetaan umunya dinotasikan dengan
f : x $\rightarrow$ y
yang dibaca fungsi f memetakan x ke y. Dimana peta dari x adalah y, selanjutnya fungsi tersebut dirumuskan dengan f(x) = y. Dalam fungsi dikenal beberapa istilah seperti domain, kodomain, range, dan bayangan atau peta. Sekarang, perhatikan kembali diagram panah pada contoh 1!Diagram panah di atas merupakan sebuah fungsi. Yang dapat dikatakan domain atau daerah asal adalah semua anggota himpunan A ={1, 2, 3, 4}. Kodomain atau daerah lawan/kawan adalah anggota semua anggota himpunan B = {1, 4, 9, 16, 25}. Sedangkan range adalah anggota kodomain yang memiliki pasangan dengan anggota domain dalam hal ini adalah {1, 4, 9, 16}
Menentukan Nilai Fungsi dan Rumus Fungsi
Untuk menentukan nilai suatu fungsi kita tinggal substitusi atau ganti variabel pada rumus fungsi dengan anggota domainnya. Untuk lebih jelasnya perhatikan contoh soal berikutContoh 3
Diketahui fungsi f dinotasikan dengan f : x $\rightarrow$ 2x + 3. Jika diketahui domain dari fungsi f adalah {0, 1, 2, 3} dan kodomainya adalah bilangan bulat. Tentukan
a. Rumus fungsi f
b. Daerah hasil f
c. Tentukan nilai x jika f(x) = 17
d. Tentukan nilai a jika f(a) = -1
Jawab
a. f(x) = 2x + 3
b. f(x) = 2x + 3
f(0) = 2(0) + 3 = 3
f(1) = 2(1) + 3 = 5
f(2) = 2(2) + 3 = 7
f(3) = 2(3) + 3 = 9
Daerah hasil = {3, 5, 7, 9}
c. f(x) = 17
2x + 3 = 17
2x = 17 - 3
2x = 14
x = 7
d. f(a) = -1
2a + 3 = -1
2a = -1 - 2
2a = -4
a = -2
Contoh 4
Jika diketahui fungsi g(x) = ax + b dengan g(2) = 4 dan g(-3) = -11, tentukan
a. Nilai a dan b
b. Rumus fungsi g
c. Peta dari 3
Jawab
a. g(x) = ax + b
g(2) = 4 maka 2a + b = 4
g(-3) = -11 maka -3a + b = -11
Eliminasi b
2a + b = 4
-3a + b = -11 -
5a = 15
a = 3
Substitusi a = 3 ke 2a + b = 4
2(3) + b = 4
6 + b = 4
b = 4 - 6
b = -2
Jadi, nilai a = 3 dan b = -2
b. g(x) = 3x - 2
c. g(x) = 3x -2
g(3) = 3(3) - 2 = 7
Jadi, peta dari 3 adalah 7
Menentukan Banyaknya Fungsi yang Dapat Dibuat dari Dua Himpunan
Untuk menentukkan banyaknya suatu fungsi yang mungkin dapat dibuat dari dua himpunan kita dapat menggunakan sebuah rumus. Misalkan himpunan A dan himpunan B dengan jumlah anggota A adalah n(A) dan jumlah anggota himpunan B adalah n(B), banyaknya fungsi atau pemetaan dari himpunan A ke himpunan B yang dapat dibuat adalah
A ke B = n(B)$^{n(A)}$
Sedangkan, banyaknya pemetaan dari himpunan B ke himpunan A yang dapat dibuat adalah
B ke A = n(A)$^{n(B)}$
Contoh 5
Diketahui himpunan A = {himpunan pembentuk kata CERIA} dan himpunan B = {bilangan prima kurang dari 10}. Tentukan banyaknya
a. Pemetaan dari himpunan A ke B
b. Pemetaan dari himpunan B ke A
Jawab
A ={ C, E, R, I, A}
n(A) = 5
B = {2, 3, 5, 7}
n(B) = 4
a. A ke B = n(B)$^{n(A)}$ = 4$^{5}$ = 1024
b. B ke A = n(A)$^{n(B)}$ = 5$^{4}$ = 625
Contoh 6
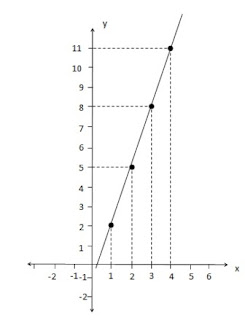
Buatlah gambar grafik fungsi f(x) = 3x - 1 dengan domain dan kodomain merupakan bilangan real!
Jawab
f(x) = 3x - 1
Tabel fungsi

Grafik fungsi
Demikianlah mengenai fungsi atau pemetaan, semoga bermanfaat.
Jawab
A ={ C, E, R, I, A}
n(A) = 5
B = {2, 3, 5, 7}
n(B) = 4
a. A ke B = n(B)$^{n(A)}$ = 4$^{5}$ = 1024
b. B ke A = n(A)$^{n(B)}$ = 5$^{4}$ = 625
Menggambar Grafik Fungsi
Untuk menggambar grafik suatu fungsi pada bidang carteius, kita tinggal menentukan beberapa titik sembarang atau nilai x. Setelah menentukan nilai x, kemudian buat tabel bantu yang akan kita gunakan sebagai acuan dalam menggambar grafik. Untuk lebih jelasnya perhatikan contoh soal berikut
Contoh 6
Buatlah gambar grafik fungsi f(x) = 3x - 1 dengan domain dan kodomain merupakan bilangan real!
Jawab
f(x) = 3x - 1
Tabel fungsi

Grafik fungsi

Demikianlah mengenai fungsi atau pemetaan, semoga bermanfaat.

Post a Comment for "Mengenal Fungsi atau Pemetaan dan Contoh Soalnya"
Terima kasih atas komentar yang telah anda berikan