Soal-Soal Pythagoras dan Pembahasannya

 Berikut ini adalah 20 butir soal-soal Pythagoras dan pembahasannya dengan tipe soal pilihan ganda. Beberapa sub materi soal Pythagoras yang dibahas adalah mengenai konsep Pythagoras, Mencari panjang sisi-sisi segitiga siku-siku, Triple Pythagoras, Penerapan Triple Pythagoras dalam menentukan jenis segitiga, Penerapan Pythagoras dalam kehidupan sehari-hari, dan Perbandingan sisi-sisi segitiga siku-siku dengan sudut istimewa (30$^o$, 45$^{o}$, dan 60$^{o}$}.

Contoh Soal Pythagoras dan Pembahasannya

Soal 1
jika a adalah sisi miring segitiga siku-siku, b dan c adalah sisi lainnya, maka berlaku teorema phytagoras dengan rumus?
A. $a^{2} + b^{2} = c^{2}$
B. $a^{2} + c^{2} = b^{2}$
C. $b^{2} + c^{2} = a^{2}$
D. $b^{2} - c^{2} = a^{2}$

Pembahasan
Pada segitiga siku-siku berlaku bahwa kuadrat sisi miring (hipotenusa) sama dengan jumlah kuadrat dua sisi yang lainnya, maka pada soal di atas yang benar adalah
C. $b^{2} + c^{2} = a^{2}$

Soal 2
 Apa nama lain dari Hipotenusa ?
A. Sisi samping
B. Pythagoras
C. Sisi tegak
D. Sisi miring

Pembahasan
D. Sisi miring

Soal 3
Rumus phytagoras yang tepat untuk gambar di bawah ini adalah...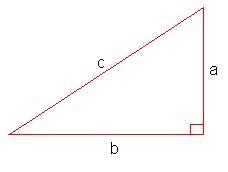

A. $c^{2} = a^{2} + b^{2}$
B. $c^{2} = a^{2} - b^{2}$
C. $a^{2} = c^{2} + b^{2}$
D. $b^{2} = c^{2} + a^{2}$

Pembahasan
A. $c^{2} = a^{2} + b^{2}$

Soal 4
Berdasarkan teorema Pythagoras, pada segitiga siku-siku, kuadrat panjang sisi miring sama dengan......
A. Selisih kuadrat panjang sisi siku-sikunya
B. Jumlah kuadrat panjang sisi siku-sikunya

C. Selisih akar panjang sisi siku-sikunya
D. Jumlah akar panjang sisi siku-sikunya

Pembahasan
B. Jumlah kuadrat panjang sisi siku-sikunya

Soal 5
Panjang t pada segitiga siku-siku di bawah ini adalah...

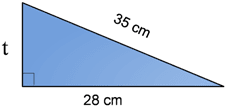
A. 21 cm
B. 24 cm
C. 25 cm
D. 26 cm

Pembahasan
$t = \sqrt{35^{2} - 28^{2}}$

$t = \sqrt{1225 - 784}$

$t = \sqrt{441}$
$t = 21$ cm
Jadi, panjang t adalah 21cm

Soal 6
Panjang AD pada gambar bangun di bawah adalah ...

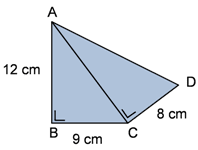
A. 13 cm
B. 17 cm
C. 23 cm
D. 27 cm

Pembahasan
Untuk mendapatkan panjang AD maka kita dapat memanfaatkan segitiga siku-siku ACD, tapi sisi AC belum diketahui. Maka dari itu hal pertama yang dilakukan adalah mencari sisi AC dengan memanfaatkan segitiga siku-siku ABC

$AC = \sqrt{AB^{2} + BC^{2}}$
$AC = \sqrt{12^{2} + 9^{2}}$
$AC = \sqrt{144 + 81}$

$AC = \sqrt{225}$
$AC = 15 cm$

Selanjutnya kita akan mencari AD

$AD = \sqrt{AC^{2} + CD^{2}}$
$AD = \sqrt{15^{2} + 8^{2}}$

$AD = \sqrt{225 + 64}$
$AD = \sqrt{289}$
$AD = 17 cm $
Jadi, panjang AD adalah 17 cm

Soal 7
Panjang PQ pada gambar bangun di bawah adalah ...

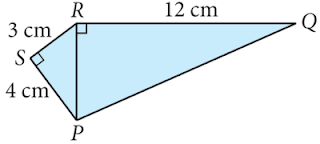
A. 9 cm
B. 11 cm
C. 13 cm
D. 15 cm

Pembahasan
Untuk mendapatkan panjang PQ maka kita dapat memanfaatkan segitiga siku-siku PQR, tapi sisi PR belum diketahui. Maka dari itu hal pertama yang dilakukan adalah mencari sisi PR dengan memanfaatkan segitiga siku-siku PRS

$PR = \sqrt{PS^{2} + RS^{2}}$
$PR = \sqrt{4^{2} + 3^{2}}$
$PR = \sqrt{16 + 9}$

$PR = \sqrt{25}$
$PR = 5 cm$

Selanjutnya kita akan mencari AD

$PQ = \sqrt{QR^{2} + PR^{2}}$
$PQ = \sqrt{12^{2} + 5^{2}}$

$PQ = \sqrt{144 + 25}$
$PQ = \sqrt{169}$
$PQ = 13 cm $
Jadi, panjang PQ adalah 13 cm

Soal 8

Perhatikah bangun di bawah yang terdiri dari jajar genjang dan segitiga siku-siku. Keliling bangun tersebut adalah ….

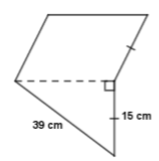
A. 105 cm
B. 120 cm
C. 123 cm
D. 156 cm

Pembahasan

Untuk memudahkan menyelesaikan soal di atas, kita perlu menamakan titik-titik sudut dari bangun di atas

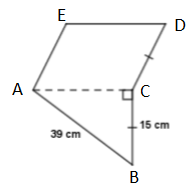
Dari gambar diketahui BC = CD = 15 cm, dan karena ACDE merupakan jajar genjang maka CD = AE = 15 cm. Langkah berikutnya yang kita lakukan adalah menentukan panjang DE, dimana DE = AC karena ACDE merupakan bangun jajargenjang.
$AC= \sqrt{AB^{2} - BC^{2}}$
$AC = \sqrt{39^{2} - 15^{2}}$
$AC = \sqrt{1521 - 225}$
$AC = \sqrt{1296}$
$AC = 36$ cm
Sehingga diperoleh DE = 36 cm

Keliling bangun = AB + BC + CD + DE + AE
Keliling bangun = 39 +15 + 15 + 36 + 15

Keliling bangun = 120 cm
Jadi, keliling bangun adalah 120 cm

Soal 9

Pada gambar berikut, luas ΔPQR = 72 cm$^{2}$ dan PT : TQ = 3 : 1. Jika tinggi RT = 12 cm, PR = .....

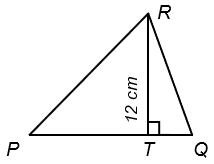
A. 20 cm
B. 17 cm
C. 15 cm
D. 13 cm

Pembahasan
Langkah pertama yang dilakukan adalah mencari PT, dimana kita akan memanfaatkan luas ΔPQR

$Luas PQR = \frac{1}{2} \times PQ \times RT$

$Luas PQR = 72$

$ \frac{1}{2} \times PQ \times RT = 72$
$ \frac{1}{2} \times PQ \times 12 = 72$

$ 6 \times PQ = 72$
$ PQ = \frac{72}{6}$

$PQ = 12$ cm

Karena PT : TQ = 3 : 1 maka berlaku
$PT = \frac{3}{3 + 1} \times PQ$
$PT = \frac{3}{4} \times 12$
$PT = 9$ cm

$PR = \sqrt{PT^{2} + RT^{2}}$

$PR = \sqrt{9^{2} + 12^{2}}$

$PR = \sqrt{81 + 144}$

$PR = \sqrt{225}$

$PR = 15$ cm
Jadi, panjang sisi PR = 15 cm

Soal 10
Sebuah segitiga siku-siku PQR memiliki panjang hipotenusa 25 cm. salah satu panjang garis tegak lurusnya adalah 24 cm. Panjang sisi lainnya adalah...
A. 7 cm|
B. 8 cm

C. 11 cm

D. 12 cm

Pembahasan
Misalkan panjang sisi yang dicari adalah x, maka

$x = \sqrt{25^{2} - 24^{2}}$
$x = \sqrt{625 - 576}$

$x = \sqrt{49}$

$x = 7$ cm
Jadi, panjang sisi lainnya adalah 7 cm

Soal 11
Tripel phytagoras 3x, 12, 5x. Yang terbesar adalah 5x. Nilai x adalah...
A. 3
B. 6

C. 12
D. 15

Pembahasan
Karena merupakan triple Pythagoras dan 5x merupakan sisi terpanjang/terbesar maka berlaku
$(5x)^{2} = (3x)^{2} + 12^{2}$
$25x^{2} = 9x^{2} + 144$
$25x^{2} - 9x^{2} = 144$
$16x^{2} = 144$
$x^{2} = \frac{144}{16}$
$x^{2} = 9$
$x = \sqrt{9}$
$x = 3$
Jadi, nilai x adalah 3

Soal 12
Perhatikan gambar bangun di bawah, Bangun PQRST terdiri atas persegi panjang dan segitiga siku-siku. Luas bangun tersebut adalah ...

A. 806 cm$^2$
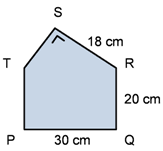
B. 816 cm$^2$
C. 846 cm$^2$
D. 854 cm$^2$

Pembahasan
Langkah pertama kita cari terlebih dahulu ST 

$ST = \sqrt{RT^{2} - SR^{2}}$
$ST = \sqrt{30^{2} - 18^{2}}$
$ST = \sqrt{900 - 324}$
$ST = \sqrt{576}$
$ST = 24$ cm

Luas PQRST = Luas RST + Luas PQRT
Luas PQRST $= \frac{1}{2} \times ST \times RS + PQ \times RT$
Luas PQRST $= \frac{1}{2} \times 24 \times 18 + 30 \times 20$

Luas PQRST $=  12 \times 18 + 600$
Luas PQRST $=  216 + 600$
Luas PQRST $=  816$ cm$^2$
Jadi, luas bangun PQRST adalah 816 cm$^2$

Soal 13

Diketahui empat pasang bilangan sebagai berikut :

(i) 20, 15, 25

(ii) 14, 48, 50

(iii) 15, 17, 24

(iv) 20, 29, 21

Dari empat pasang bilangan di atas, yang merupakan tripel phytagoras adalah .....
A. (i), (ii), (iii)
B. (i), (iv)
C. (ii), (iii), (iv)
D. (i), (ii), (iv)

Pembahasan
Untuk menguji suatu triple pythagoras maka dapat dilakukan dengan berpedoman bahwa kuadrat sisi terpanjang/ terbesar merupakan jumlah kuadrat sisi/angka lainnya

(i) 20, 15, 25
$25^{2} = 20^{2} + 15^{2}$
$625 = 400 + 225$
$625 = 625$ (Triple Pythagoras)

(ii) 14, 48, 50
$50^{2} = 14^{2} + 48^{2}$

$2500 = 196 + 2304$
$2500 = 2500$ (Triple Pythagoras)

(iii) 15, 17, 24

$24^{2} = 15^{2} + 17^{2}$

$576 = 225 + 289$
$576 \neq 514$ (bukan Triple Pythagoras)

(iv) 20, 29, 21

$29^{2} = 20^{2} + 21^{2}$

$841 = 400 + 441$
$841 = 841$ (Triple Pythagoras)

Jadi, yang termasuk sebagai triple Pythagoras adalah (i), (ii), dan (iv)

Soal 14
Jenis segitiga untuk ukuran 15 cm, 20 cm, dan 25 cm adalah...
A. Segitiga Tumpul
B. Segitiga Lancip
C. Segitiga Siku-Siku
D. Segitiga Sama Kaki

Pembahasan
$25^{2} = 20^{2} + 15^{2}$
$625 = 400 + 225$
$625 = 625$
Jadi, segitiga dengan ukuran panjang sisi-sisinya 15 cm, 20 cm, dan 25 cm merupakan segitiga siku-siku

Soal 15
Diketahui ukuran sebuah segitiga 10 cm, 24 cm, dan 27 cm, maka segitiga tersebut adalah segitiga....
A. Segitiga Lancip
B. Segitiga Tumpul
C. Segitiga Siku-Siku
D. Segitiga Sama Kaki

Pembahasan
$27^{2} = 24^{2} + 10^{2}$
$729 = 576 + 100$
$729 > 676$
Jadi, segitiga dengan ukuran panjang sisi-sisinya 10 cm, 24 cm, dan 27 merupakan segitiga Tumpul

Soal 16
Dua buah tiang berdampingan berjarak 12 m. Jika tinggi tiang masing-masing adalah 22 m dan 13 m. Panjang kawat penghubung antara ujung kedua tiang tersebut adalah ...
A. 15 m
B. 16 m

C. 17 m

D. 18 m

Pembahasan
Soal di atas dapat diilustrasikan sebagai berikut!

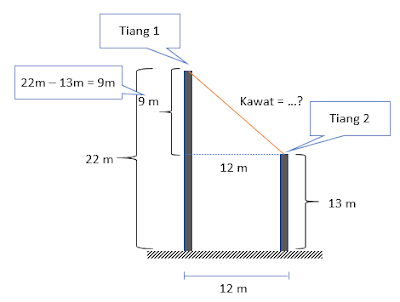
Dengan demikian, misalkan panjang kawat adalah x, maka

$x = \sqrt{12^{2} + 9^{2}}$
$x = \sqrt{144 + 81}$

$x = \sqrt{225}$
$x = 15 $ m
Jadi, panjang kawat penghubung antara ujung kedua tiang tersebut adalah 15 m

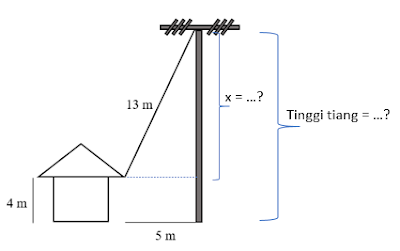
Soal 17

Tiang sebuah antena televisi diikat menggunakan kawat seperti pada gambar di bawah. Tinggi antena tersebut ... 

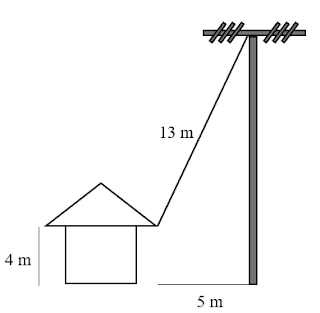
A. 12 m

B. 14 m

C. 16 m

D. 18 m

Pembahasan
Dari soal dapat kita ilustrasikan, sebagai berikut

Langkah pertama, kita cari dulu x

$x = \sqrt{13^{2} - 5^{2}}$
$x = \sqrt{169 - 25}$

$x = \sqrt{144}$

$x = 12$ m

Berikutnya, kita tentukan tinggi tiang
Tinggi Tiang = 12 + 4 = 16 m
Jadi, tinggi tiang listrik adalah 16 m

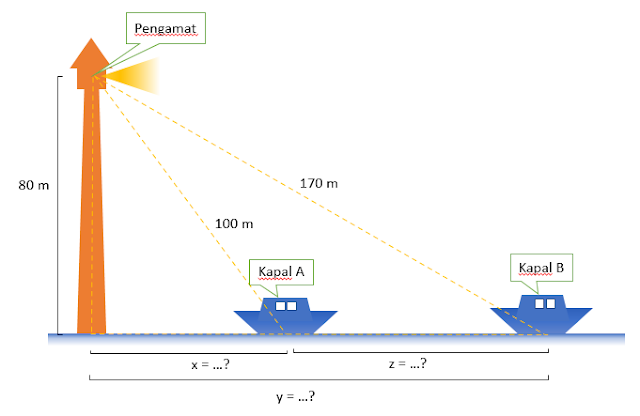
Soal 18
Seorang pengamat berada di atas sebuah mercusuar yang memiliki ketinggian 80 meter. Pengamat melihat kapal A dan kapal B. Jarak pengamat ke kapal A 100 meter dan jarak pengamat ke kapal B 170 meter. Posisi alas mercusuar, kapal A, dan kapal B segaris. Jarak antara kapal A dan kapal B adalah ….
A. 70 m
B. 80 m
C. 90 m

D. 110 m

Pembahasan
Misalkan x adalah jarak antara kapal A dengan dasar mercusuar, y adalah jarak antara kapal B dengan dasar mercusuar, dan z dalah jarak antara kapal A dan kapal B, maka dapat diilustrasikan sebagai berikut:

Pertama kita akan mencari nilai x yaitu jarak Mercusuar dengan Kapal A
$x = \sqrt{100^{2} - 80^{2}}$

$x = \sqrt{10000 - 6400}$
$x = \sqrt{3600}$
$x = 60$ m

Kemudian mencari nilai y yaitu jarak Mercusuar dengan Kapal B
$y =\sqrt{170^{2} - 80^{2}}$
$y = \sqrt{28900 - 6400}$
$y = \sqrt{22500}$
$y = 150$ m

Sehingga nilai z yaitu jarak Kapal A dengan Kapal B adalah
$z = y - x$
$z = 150 - 60$
$z = 90$ m
Jadi, jarak antara Kapal A dengan Kapal B adalah 90 m

Soal 19
 Perhatikan gambar berikut! Jika panjang sisi miring 30 cm, maka panjang sisi tegak dan sisi datarnya adalah ...

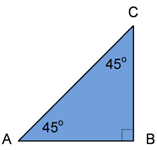
A. 15 cm
B. $15\sqrt{2}$ cm
C. $30\sqrt{2}$ cm
D. 30 cm

Pembahasan

Karena dua sudutnya 45$^o$ maka berlaku perbandingan sisi-sisinya
AB : BC : AC = 1 : 1 : $\sqrt{2}$

$BC = \sqrt{1}{\sqrt{2}} \times AC$
$BC = \sqrt{1}{\sqrt{2}} \times 30$
$BC = \sqrt{30}{\sqrt{2}}$
$BC =  \sqrt{30}{\sqrt{2}} \times  \sqrt{\sqrt{2}}{\sqrt{2}}$ kalikan bentuk sekawan penyebut
$BC = \sqrt{30 \sqrt{2}}{2}$
$BC = 15 \sqrt{2}$
Jadi, panjang sisi tegaknya adalah $15 \sqrt{2}$

Soal 20
Diketahui panjang $AC = 42\sqrt{3}$ cm. Panjang AB adalah ...

A. 21 cm
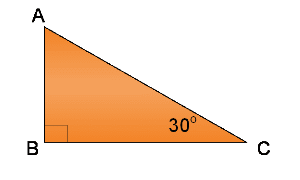
B. 42 cm
C. $21\sqrt{3}$ cm
D. $24\sqrt{3}$ cm

Pembahasan

Karena salah satu sudut segitiga siku-siku ABC yaitu sudut C = 30$^{o}$ maka berlaku perbandingan sisi-sisinya
AB : BC : AC = 1 : $\sqrt{3}$ : 2

$AB = \sqrt{1}{2} \times AC$
$AB = \sqrt{1}{2} \times 42\sqrt{3}$
$AB = 21\sqrt{3}$ cm
Jadi, panjang AB = $21\sqrt{3}$ cm

Demikianlah, mengenai contoh soal Pythagoras dan pembahasannya, semoga bermanfaat.

Share :